Neka su date dve nejednake veličine. Ako od veće oduzmemo veličinu veću od polovine, a od ostatka - veću od njegove polovine i tako postupamo neprekidno, ostaće neka veličina koja je manja od date manje veličine.

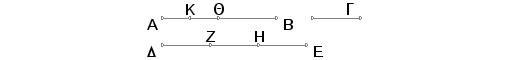
Neka su date dve nejednake veličine AB i G, od kojih je AB veća. Tvrdim da će, ako od AB oduzmemo veličinu veću od polovine i od ostatka - veću od njegove polovine i tako postupamo neprekidno, ostati neka veličina manja od G.
Zaista, veličina G ponovljena više puta daje jednom veličinu veću od AB. Izvršimo to ponavljanje, i neka je DE multiplum G veći od AB. Podelimo DE na delove DZ, ZH, HE jednake veličine G i oduzmimo od AB veličinu AQ veću od polovine AB, a od AQ veličinu QK veću od polovine AQ i tako postupimo neprekidno, dok broj podelaka na AB ne bude jednak broju podelaka na DE.
Neka je sad broj podelaka AK, KQ, QB jednak broju podelaka DZ, ZH, HE. Pošto je DE veće od AB, i od DE se oduzima veličina EH manja od polovine DE, a od AB veličina BQ veća od polovine AB, biće ostatak HD veći od ostatka QA. I pošto je HD veće od QA i od HD se oduzima polovina HZ, a od QA veličina QK veća od polovine, biće i ostatak DZ veći od ostatka AK. Ali DZ je jednako G. Znači i G je veće od AK. Pa prema tome je AK manje od G.
Na taj način ostaje od AB veličina AK manja od date manje veličine G. A to je trebalo dokazati. - Slično se dokazuje, kad se oduzimaju polovine.