105.

Duž samerljiva sa manjom (iracionalom) je manja.

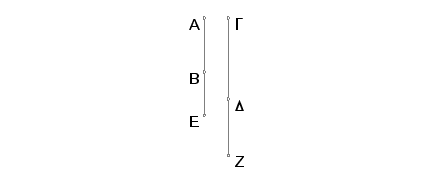
Neka je AB manja i GD duž samerljiva sa AB. Tvrdim da je i GD manja.
Zaista, uradimo isto što i ranije. I pošto su duži AE i EB nesamerljive u stepenu, biće GZ i ZD nesamerljive u stepenu. Sad, pošto je AE prema EB kao GZ prema ZD, biće i kvadrat na AE prema kvadratu na EB kao kvadrat na GZ prema kvadratu na ZD. I, posle spajanja, zbir kvadrata na AE i na EB je prema kvadratu na EB kao zbir kvadrata na GZ i na ZD prema kvadratu na ZD (i sa permutacijom). No kvadrat na BE je samerljiv sa kvadratom na ZD. No zbir kvadrata na AE i na EB je racionalan, zbog toga je i zbir kvadrata na GZ i na ZD racionalan. Zatim, pošto je kvadrat na AE prema pravougaoniku sa stranama AE i EB kao kvadrat na GZ prema pravougaoniku sa stranama GZ i ZD, a kvadrat na AE je samerljiv sa kvadratom na GZ, biće samerljiv i pravougaonik kome su strane AE i EB sa pravougaonikom kome su strane GZ i ZD. No pravougaonik sa stranama AE i EB je medijalan, znači medijalan je i pravougaonik sa stranama GZ i ZD. Prema tome su duži GZ i ZD nesamerljive u stepenu i zbir kvadrata obrazovanih na njima je racionalan, a pravougaonik od njih medijalan.
Na ovaj način GD je manja (iracionala). A to je trebalo dokazati.