106.
Duž samerljiva sa "duži koja sa racionalnom obrazuje celo medijalno" je duž koja sa racionalnomobrazuje celo medijalno.
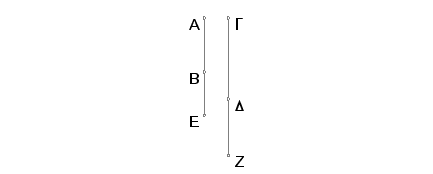
Neka je AB duž koja sa racionalnom obrazuje medijalno i GD duž samerljiva sa AB. Tvrdim da ja GD duž koja sa racionalnom obrazuje celo medijalno.
Zaista, neka je BE dodatak za AB. Tada su AE i EB duži nesamerljive u stepenu, one obrazuju medijalan zbir kvadrata na AE i na EB i racionalna pravougaonik sa ovim stranama. I uradimo isto što i ranije. Slično prethodnom se dokazuje da su GZ i ZD u istoj razmeri kao i AE i EB i da je zbir kvadrata na AE i na EB samerljiv sa zbirom kvadrata na GZ i na ZD, a pravougaonik kome su strane AE i EB samerljiv sa pravougaonikom kome su strane GZ i ZD. Prema tome su duži GZ i ZD nesamerljive u stepenu i obrazuju medijalan zbir kvadrata na GD i racionalan pravougaonik od njih.
Na ovaj način, GD je duž koja sa racionalnom obrazuje celo medijalno. A to je trebalo dokazati.