113.

Kvadrat na racionalnoj duži, konstruisan na apotomi ima za širinu binomijalu, čije su racionale samerljive sa racionalama apotome i u istoj su razmeri, i tako dobivena binomijala je istoga reda kao i apotoma.

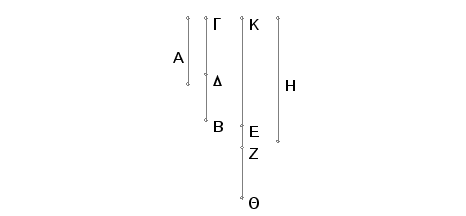
Neka je A racionalna duž, BD - apotoma, i kvadrat na A neka je jednak pravougaoniku sa stranama BD i KQ, tako da kvadrat na racionalnoj duži A, konstruisan, kao pravougaonik, na apotomi BD ima za širinu duž KQ. Tvrdim, da je KQ binomijala, čije su racionale samerljive sa racionalama apotome BD i u istoj razmeri i da je KQ istoga reda kao i BD.
Zaista, neka je DG dodatak za BD. Tada su duži BG i GD racionalne i samerljive samo u stepenu. I kvadrat na A jednak je pravougaoniku sa stranama BG i H. A kako je kvadrat na A racionalan, biće racionalan i pravougaonik sa strnama BG i H. I konstruisan je na racionalnoj duži BG. Zbog toga je racionalan i duž H i samerljiva po dužini sa BG. Pošto je sad pravougaonik sa stranama BG i H jednak pravougaoniku sa stranama BD i KQ, postoji proporcija: BG je prema BD kao KQ prema H. No BG je veće od BD, pa znači i KQ je veće od H. Uzmimo KE jednako H, znači KE je samerljivo po dužini sa BG. I pošto je GB prema BD kao QK prema KE, biće, posle zamene jednog dela drugim, BG prema GD kao KQ prema QE. Načinimo tako da KQ bude prema QE kao QZ prema ZE, pa će i ostatak KZ biti prema ZQ kao KQ prema QE, tj. kao BG prema GD. No duži BG i GD samerljivo samo u stepenu, pa prema tome i duži KZ i ZQ biće samerljive samo u stepenu. I pošto je KQ prema QE kao KZ prema ZQ, to je KZ prema ZQ kao QZ prema ZE. A pošto je prvo prema trećem kao kvadrat na prvom prema kvadratu na drugom, to je i KZ prema ZE kao kvadrat na KZ prema kvadratu na ZQ. No kvadrat na KZ je samerljiv sa kvadratom na ZQ, jer su duži KZ i ZQ samerljive u stepenu. Znači KZ i ZE su samerljive po dužini, te je KZ samerljivo po dužini i sa KE. No duž KZ je racionalan i samerljiva po dužini sa BG. I pošto je BG prema GD kao KZ prema ZQ, biće, posle permutovanja, BG prema KZ kao DG prema ZQ. No BG je samerljivo sa KZ, prema tome i ZQ je samerljivo po dužini sa GD su racionalne, samerljive samo u stepenu. Zbog toga su i duži KZ i ZQ racionalne, samerljive samo u stepenu. Duž KQ je prema tome binomijala.
Ako je sad kvadrat na BG veći od kvadrata na GD za kvadrat na duži samerljivoj sa BG, biće i kvadrat na KZ veći od kvadrata na ZQ za kvadrat na duži samerljivoj sa KZ. I ako je BG samerljivo po dužini sa uzetom racionalnom duži, biće samerljivo i KZ, a ako je GD samerljivo po dužini sa uzetom racionalnom duži, biće i ZQ, a ako nijedna od BG i GD nije samerljiva, neće biti samerljiva nijedna od KZ i ZQ.
A ako je vkadrat na BG, veći od kvadrata na GD za kvadrat na duži nesamerljivoj sa BG, biće i kvadrat na KZ veći od kvadrata na ZQ za kvadrat na duži nesamerljivoj sa KZ. I ako je BG samerljivo po dužini sa uzetom racionalnom duži, biće samerljivo i KZ, a ako je GD samerljivo, biće i ZQ, a ako nijedna od BG i GD nije samerljiva, neće biti nijedna ni od KZ i ZQ.
Na ovaj način, KQ je binomijala, čije su dve racionale KZ i ZQ samerljive sa racionalama BG i GD apotome i u istoj razmeri sa njima. I KQ ima isti red sa BG. A to je trebalo dokazati.