114.

Ako je površina (pravougaonika) obuhvaćena apotomom i binomijalom čije su racionale samerljive sa racionalama apotome i u istoj razmeri, biće strana kvadrata jednakog toj površini racionalna.

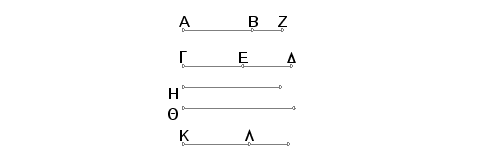
Neka je površina (pravougaonika) sa stranama AB i GD obuhvaćena apotomom AB i binomijalom GD i neka je GE veća racionala binomijale, neka su racionale GE i ED binomijale samerljive sa racionalama AZ i ZB apotome i u istoj razmeri sa njima, i neka je H strana kvadrata jednakog pravougaoniku sa stranama AB i GD. Tvrdim da je duž H racionalna.
Zaista, uzmimo racionalnu duž Q i konstruišimo na GD pravougaonik, jednak kvadratu na Q, kome je širina KL. Prema tome je KL apotoma, čije su racionale KM i ML samerljive sa racionalama GE i ED binomijale i u istoj razmeri sa njima. Prema tome je AZ prema ZB kao KM prema ML. I, posle permutovanja, AZ je prema KM kao BZ prema LM. Znači i ostatak AB je prema ostatku KL kao AZ prema KM. No AZ je samerljivo sa KM, pa znači i AB je samerljivo sa KL. I AB je prema KL kao pravougaonik sa stranama GD i AB prema pravougaoniku sa stranama GD i KL. Znači i pravougaonik sa stranama GD i AB je samerljiv sa pravougaonikom sa stranama GD i KL. No pravougaonik sa stranama GD i KL jednak je kvadratu na H. Zbog toga je pravougaonik sa stranama GD i AB samerljiv sa kvadratom na Q. Ali pravougaonik sa stranama GD i AB jednak je kvadratu na H. Znači i kvadrat na H je samerljiv sa kvadratom na Q. A kako je kvadrat na Q racionalan, biće racionalan i kvadrat na H. Znači racionalna je i duž H. I kvadrat na njoj je jednak pravougaoniku sa stranama GD i AB.
Na ovaj način, ako je površina obuhvaćena apotomom i binomijalom čije su racionale samerljive sa racionalama apotome i u istoj razmeri, biće strana kvadrata jednakog toj površini racionalna.