17.

Ako postoje dve nejednake duži i ako je na većoj konstruisan sa kvadratnom dopunom paralelogram, koji je jednak četvrtini kvadrata na manjoj, i deli tu duž na delove samerljive po dužini, biće kvadrat na većoj duži veći od kvadrata na manjoj za kvadrat duži koja je samerljiva po dužini sa većom duži. I ako je kvadrat na većoj duži veći od kvadrata na manjoj za kvadrat duži koja je samerljiv po dužini sa većom duži, i na većoj je konstruisan sa kvadratnom dopunom paralelogram koji je jednak četvrtini kvadrata na manjoj, on (paralelogram) će deliti veću duž na delove samerljive po dužini.

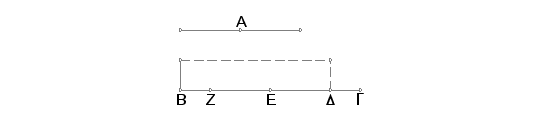
Neka su A i BG dve nejednake duži od BG je veća. I neka je na BG konstruisan sa kvadratnom dopunom paralelogram jednak četvrtini kvadrata na A, tj. kvadratu na polovini A, a sa stranama BD i DG i neka BD samerljivo po dužini sa DG. Tvrdim da je kvadrat na BG veći od kvadrata na A za kvadrat na duži samerljivoj sa BG.
Zaista, prepolovimo BG tačkom E, i odmerimo DE jednako EZ. Tada je ostatak DG jednak BZ. I pošto je duž BG podeljena tačkom E na jednake delove, a tačkom D na nejednake, biće pravougaonik sa stranama BD i DG, sa kvadratom na ED, jednak kvadratu na EG. A i učetvorostručeni, naime: četvorostruki pravougaonik sa stranama BD i DG, sa četvorostrukim kvadratom na ED, jednak je četvorostrukom kvadratu na EG. Ali četvorostruki pravougaonik sa stranama BD i DG jednak je kvadratu na A, četvorostruki kvadrat na DE jednak je kvadratu na DZ, jer je DZ dvostruko DE. I četvorostruki kvadrat na EG jednak je kvadratu na BG, jer je ponovo BG dvostruko GE. I na taj način zbir kvadrata na A i na DZ jednak je kvadratu na BG. Dakle, kvadrat na BG veći je od kvadrata na A za kvadrat na DZ. Treba dokazati da je BG samerljivo sa DZ. Zaista, pošto je BD samerljivo po dužini sa DG, biće samerljivo po dužini i BG sa GD. Ali GD je samerljivo po dužini sa GD i BZ, jer je GD jednako BZ. Prema tome je BG samerljivo po dužini sa BZ na GD. Na ovaj način BG je samerljivo po dužini i sa ostatkom ZD. I tako je kvadrat na BG veći od kvadrata na A za kvadrat na samerljivoj duži sa BG.
Neka je sad kvadrat na BG veći od kvadrata na A za kvadrat na duži samerljivoj sa BG, i neka je na BG konstruisan sa kvadratom dopunom paralelogram koji je jednak četvrtini kvadrata na A, a sa stranama BD i DG. Treba dokazati da je BD samerljivo sa DG.
Zaista, posle iste pripreme, na sličan način se dokazuje da je kvadrat na BG veći od kvadrata na A za kvadrat na ZD. No kvadrat na BG je veći od kvadrata na A za kvadrat na duži samerljivoj sa BG. Znači BG je samerljivo po dužini i sa ostatkom, zbirom BZ sa DG. No zbir BZ sa DG je samerljiv po dužini sa DG. Prema tome je i BG samerljiv po dužini sa GD. I na taj način, posle rastavljanja, BD je samerljivo po dužini sa DG.
Na ovaj način, ako postoje dve nejednake duži, itd.