Lema
Ako postoje dve duži, biće jedna prema drugoj kao kvadrat na prvoj prema pravougaoniku sa dvema ovim dužima kao stranama.
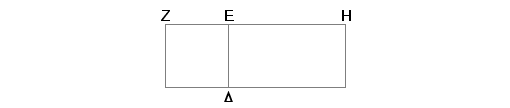
Neka su ZE i EH dve duži. Tvrdim da je ZE prema EH kao kvadrat na ZE prema pravougaoniku sa stranama ZE i EH.
Zaista, konstruišimo na ZE kvadrat DZ i dopunimo ga sa HD. I pošto je sad ZE prema EH kao ZD prema DH, i ZD je kvadrat na ZE, a DH pravougaonik sa stranama DE i EH, tj. sa ZE i EH, biće ZE prema EH kao kvadrat na ZE prema pravougaoniku sa stranama ZE i EH. Isto tako je i pravougaonik sa stranama HE i EZ prema kvadratu na EZ, tj. HD prema ZD kao HE prema EZ. A to je trebalo dokazati.