22.
Pravougaonik, jednak kvadratu na medijali, konstruisan na racionalnoj duži ima racionalnu širinu nesamerljivu po dužini sa duži na kojoj je konstruisan.
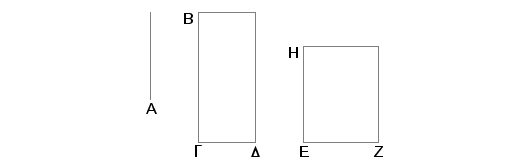
Neka je A medijala, GB racionalna duž, i neka pravougaonik BD, sa površinom jednakom površini kvadrata na A i konstruisan na BG, ima širinu GD. Tvrdim da je GD racionalno i samerljivo sa GB po dužini.
Zaista, pošto je A medijala, biće pravougaonik, čija je površina jednaka površini kvadrata na A, obuhvaćen racionalnim dužima, koje su samerljive samo u stepenu. Neka je HZ takav pravougaonik jednak kvadratu. Ali i BD je pravougaonik jednak istom kvadratu. Znači BD je jednako HZ. A oni su i sa jednakim uglovima. Ako su kod jednakih paralelograma sa jednakim uglovima kraci jednakih uglova obrnuto propocionalni, biće proporcija: BG je prema EH kao EZ prema GD. Prema tome i proporcija: kvadrat na BG je prema kvadratu na EH kao kvadrat na EZ prema kvadratu na GD. Ali kvadrat na GB je samerljiv sa kvadratom na EH, poštoje svaka od ovih duži racionalna. Znači i kvadrat na EZ je samerljiv sa kvadratom na GD. A kako je kvadrat na EZ racionalan, biće racionalan i kvadrat na GD, te prema tome je racionalna i duž GD. A pošto je EZ nesamerljivo sa EH po dužini, jer su one samerljive samo u stepenu, i EZ je prema EH kao kvadrat na EZ prema pravougaoniku sa stranama ZE i EH, biće kvadrat na EZ nesamerljiv sa pravougaonikom sa stranama ZE i EH. Ali sa kvadratom na EZ je samerljiv kvadrat na GD, jer su oni racionalniu stepenu. I pravougaonik sa stranama DG i GB je samerljiv sa pravougaonikom sa stranama ZE i EH, jer su oba jednaki kvadratu na A. Prema tome je i kvadrat na GD nesamerljiv sa pravougaonikom sa stranama DG i GB. Ali kvadratna GD je prema pravougaoniku sa stranama DG i GB kao DG prema GB. Tako je DG nesamerljivo po dužini sa GB. Na ovaj način duž GD je racionalna i nesamerljiva po dužini sa GB. A to je trebalo dokazati.