25.
Ako su strane pravougaonika medijale, samerljive samo u stepenu, biće pravougaonik ili racionalan ili medijalan. Neka su strane AB i BG pravougaonika AG medijale, a samerljive samo u stepenu. Tvrdim, da je AG ili racionalan ili medijalan.
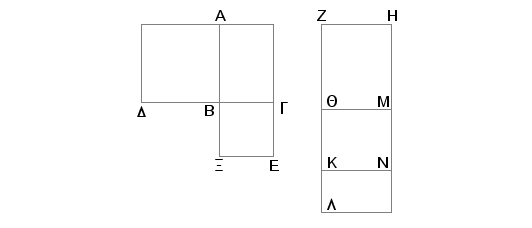
Zaista, konstruišimo na AB i BG kvadrate AD i BE. Tada je svaki od AD, BE medijalan. Odmerimo racionalnu duž ZH i konstruišimo na ZH pravougaonik HQ, jednak kvadratu AD, sa širinom ZQ, a na QM pravougaonik MK, jednak pravougaoniku AG, sa širinom QK i slično, na KN konstruišimo pravougaonik NL, jednak kvadratu BE sa širinom KL, jednak kvadratu BE, sa širinom KL. Tada su ZQ, QK, KL na pravoj. Pošto je svaki od kvadrata AD i BE medijalan, a kvadrat AD jednak je pravougaoniku HQ i kvadrat BE jednak pravougaoniku NL, biće i svaki od pravougaonika HQ i NL medijalan. A kako su oni konstruisani na racionalnoj duži ZH, biće i svaka od duži ZQ i KL racionalna i nesamerljiva po dužini sa ZH. Ali kako je AD samerljivo sa BE, biće samerljivo i HQ sa NL. Ali HQ je prema NL kao ZQ prema KL. Pa prema tome biće i ZQ samerljivo po dužini sa KL. Na ovaj način su ZQ i KL racionalne i samerljive po dužini, znači i pravougaonik obuhvaćen dužima ZQ i KL je racionalan. I pošto je duž DB jednaka BA, a XB duži BG, to je DB prema BG kao AB prema BX. Međutim DB je prema BG kao DA prema AG, pa prema tome biće i AB prema BX kao AG prema GX. Prema tome je DA prema AG kao AG prema GX. Ali kvadrat AD jednak je pravougaoniku HQ, a pravougaonik AG pravougaoniku MK i kvadrat GX pravougaoniku NL. Na ovaj način HQ je prema MK kao MK prema NL. Te, prema tome, i ZQ je prema QK kao QK prema KL. Znači pravougaonik sa stranama ZQ i KL jednak je kvadratu na QK. Ali pravougaonik sa stranama ZQ i KL je racionalan, pa će onda i kvadrat na QK biti racionalan, a to znači i duž QK racionalna. I ako je ona samerljiva pod dužini sa ZH, biće i pravougaonik QN racionalan. A ako je ona nesamerljiva po dužini sa ZH biće KQ i QM racionalne, ali samerljive samo u stepenu. Na ovaj način je pravougaonik QN ili racionalan ili medijalan. A ako je QN jednako AG, biće i pravougaonik AG ili racionalan ili medijalan, Na ovaj način, ako su strane pravougaonika medijalne, itd.