26.

Medijalna površina ne može biti veća od druge medijalne površine za neku racionalnu površinu.

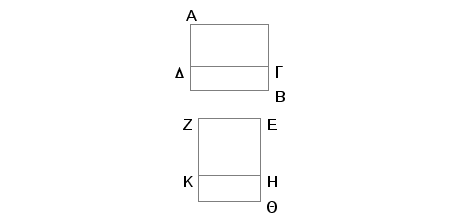
Zaista, neka bude, ako je moguće, medijalna površina AB veća od medijalne površine AG za racionalnu površinu DB, i neka je EZ racionalna duž i na duži EZ sa širinom EQ konstruisan pravougaonik ZQ sa površinom jednakom površini AB, pa oduzmimo pravougaonik ZH jednak pravougaoniku AG. Tada je ostatak BD jednak ostatku KQ. A kako je DB racionalna površina, biće racionalna i površina KQ. Pošto je svaka od površina AB i AG medijalna, i AB jednaka ZQ, a AG jednaka ZH, znači i svaka od površina ZQ i ZH je medijalna, a konstruisana na racionalnoj duži EZ. Prema tome je svaka od QE i EH racionalna i nesamerljiva po dužini sa EZ. A pošto je DB racionalna i jednaka KQ, biće i KQ racionalna, a konstruisana je na racionalnoj duži EZ. Prema tome je HQ racionalna i samerljiva po dužini sa EZ. Ali i EH je racionalna i nesamerljiva po dužini sa EZ. Na taj način EH je nesamerljiva po dužini sa HQ. Međutim EH je prema HQ kao kvadrat na EH prema pravougaoniku sa stranama EH i HQ. Pa prema tome je kvadrat na EH nesamerljiv sa pravougaonikom kome su strane EH i HQ. Ali sa kvadratom na EH samerljivi su kvadrati na EH i na HQ, jer su oni racionalni. Međutim sa pravougaonikom kome su strane EH i HQ je samerljiv i dvostruki pravougaonik sa stranama EH i HQ, jer je on dvaput veći od njega. Prema tome su kvadrati na EH i na HQ nesamerljivi sa dvostrukim pravougaonikom sa stranama EH i HQ. A to znači da su zajedno uzeti kvadrati na EH i na HQ sa dvaput uzetim pravougaonikom kome su strane EH i HQ - a to je kvadrat na EQ - nesamerljivi sa kvadratima na EH i na HQ. Ali kvadrati na EH i na HQ su racionalni, pa prema tome je kvadrat na EQ iracionalan, znači iracionalna i duž EQ, a onda je i racionalna. A to je nemoguće.
Na ovaj način, medijalna površina ne može biti veća od druge medijalne površine za neku racionalnu površinu. A to je trebalo dokazati.