28.
Naći medijale, samerljive samo u stepenu, koje su strane medijalnog pravougaonika.
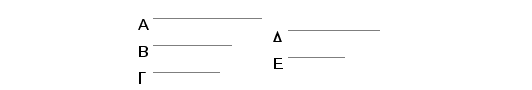
Uzmimo tri racionalne, samo u stepenu samerljive, duži A, B, G, konstruišimo za A i B srednje proporcionalnu duž D i načinimo da bude B prema G kao D prema E.
Pošto su A i B racionalne duži samerljive samo u stepenu biće pravougaonik u kome su strane A i B, jednak kvadratu na D, medijalan. Na ovaj način D je medijala. I pošto su B i G samerljive samo u stepenu, i B je prema G kao D prema E, biće prema tome i D i E samerljive samo u stepenu. A kako je D medijala, biće i E medijala. Na taj način su D i E medijale samerljive samo u stepenu. Tvrdim da je i pravougaonik, kome su one strane, medijalan. Zaista, pošto je B prema G kao D prema E, biće, posle permutovanja, B prema D kao G prema E. Ali B je prema D i kao D prema A. Znači D je prema A kao G prema E. Prema tome je pravougaonik sa stranama A i G jednak pravougaoniku sa stranama D i E. Ali pravougaonik sa stranama A i G je medijalan, pa će tada i pravougaonik sa stranama D i E biti medijalan.
Na ovaj način su nađene medijale, samerljive samo u stepenu, strane medijalnog pravougaonika. A to je trebalo dokazati.