30.

Naći dve, samo u stepenu samerljive, takve, racionalne duži da kvadrat na većoj bude veći od kvadrata na manjoj za kvadrat na duži koja je nesamerljiva po dužini sa većom.

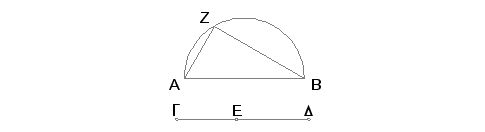
Uzmimo neku racionalnu duž AB i dva takva kvadratna broja, GE i GD, da njihov zbir GD ne bude kvadrat; i nacrtajmo na AB polukrug AZB. Pa načinimo tako da bude DG prema GE kao kvadrat na BA prema kvadratu na AZ i spojmo Z sa B.
Slično prethodnom dokazuje se da su BA i AZ racionalne i samerljive samo u stepenu. I pošto je DG prema GE kao kvadrat na BA prema kvadratu na AZ, biće posle zamene jednog dela drugim GD prema DE kao kvadrat na AB prema kvadratu na BZ. No GD prema DE nije u razmeri kao kvadratni broj prema kvadratno broju. Znači ni kvadrat na AB prema kvadratu na BZ nije u razmeri kao kvadratni broj prema kvadratnom broju. Na ovaj način AB je nesamerljivo po dužini sa BZ. I prema tome kvadrat na AB je veći od kvadrata na AZ za kvadrat na duži ZB nesamerljivoj sa AB.
Na ovaj način su AB i AZ racionalne duži, samerljive samo u stepenu, i kvadrat na AB je veći od kvadrata na AZ za kvadrat na duži ZB, koja je nesamerljiva sa AB. A to je trebalo dokazati.