32.

Naći dve medijale samerljive samo u stepenu tako da budu strane medijalnog pravougaonika i da kvadrat na većoj bude veći od kvadrata na manjoj za kvadrat na duži samerljivoj sa većom.

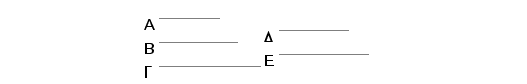
Uzmimo tri racionalne duži A, B, G samerljive samo u stepenu i to takve da je kvadrat na A veći od kvadrata na G za kvadrat na duži samerljivoj sa A. I neka je pravougaonik sa stranama A i B jednak kvadratu na D. Prema tome je kvadrat na D medijalan, a sama duž D je medijala. Neka je pravougaonik sa stranama B i G jednak pravougaoniku sa stranama D i E. I pošto je pravougaonik sa stranama A i B prema pravougaoniku sa stranama B i G kao A prema G, a pravougaonik sa stranama A i B jednak je kvadratu na D, sem toga pravougaonik sa stranama B i G jednak je pravougaoniku sa stranama D i E, biće A prema G kao kvadrat na D prema pravougaoniku sa stranama D i E. No kvadrat na D prema pravougaoniku sa stranama D i E je kao D prema E. I na ovaj način je A prema G kao D prema E. Ali A je samerljivo sa G samo u stepenu,te znači i D je samerljivo sa E samo u stepenu. I D je medijala te je prema tome i E medijala. I pošto je A prema G kao D prema E, a kvadrat na A je veći od kvadrata na G za kvadrat na duži samerljivoj sa A, biće i kvadrat na D veći od kvdarata na E za kvadrat na duži samerljivoj sa D. I tvrdim, da je pravougaonik obuhvaćen dužima D i E medijalan. Zaista, pošto je pravougaonik kome su strane B i G jednak pravougaoniku sa stranama D i E, a pravougaonik sa stranama B i G medijalan (jer su B i G racionalne i samerljive samo u stepenu) biće i pravougaonik sa stranama D i E medijalan.
Na ovaj način su nađene dve medijale D i E, samerljive samo u stepenu,koje strane medijalnog pravougaonika i kvadrat na većoj je veći od kvadrata na manjoj za kvadrat na duži samerljivoj sa D.
Slično se zatim dokazuje i za nesamerljivu duž, ako je kvadrat na A veći od kvadrata na G za kvadrat na duži nesamerljivoj sa A.