Lema
Neka je ABG pravougli trougao sa pravim uglom A i neka je A D normala. Tvrdim, da je pravougaonik sa stranama GB i BD jednak kvadratu na BA, pravougaonik sa stranama BG i GD jednak kvadratu na GA, i pravougaonik sa stranama BD i DG jednak kvadratu na AD, i još pravougaonik sa stranama BG i AD jednak je pravougaoniku sa stranama BA i AG.
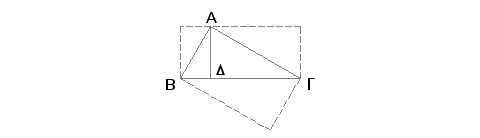
Prvo, pravougaonik sa stranama GB i BD jednak je kvadratu na BA. Zaista, pošto je AD povučeno u pravouglom trouglu iz pravog ugla normalnog na osnovu, biće trouglovi ABD i ADG slični i celom trouglu ABG i među sobom. I kako je trougao ABG sličan trouglu ABD, biće GB prema BA kao BA prema BD. Prema tome je pravougaonik sa stranama GB i BD jednak kvadratu na AB. Iz istih razloga je pravougaonik sa stranama BG i GD jednak kvadratu na AG. I pošto je u pravouglom trouglu iz pravog ugla spuštena normala na osnovu srednja proporcionalna odsečka osnove, biće BD prema DA kao AD prema DG. Pa je na taj način pravougaonik kome su stane BD i DG jednak kvadratu na DA. Tvrdim još i da je pravougaonik sa stranama BG i AD jednak pravougaoniku sa stranama BA i AG. Zaista, pošto je kako smo naveli,trougao ABG sličan trouglu ABD, biće BG prema GA kao BA prema AD(a ako su četiri duži proporcionalne, pravougaonik na srednjima je jednak pravougaoniku na krajnjima). Na ovaj način je pravougaonik na BG i AD jednak pravougaoniku na BA i AG. A to je trebalo i dokazati.