34.

Naći dve duži nesamerljive u stepenu, takve da površina sastavljena od kvadrata na njima bude medijalna, a pravougaonik obuhvaćen tim dužima racionalan.

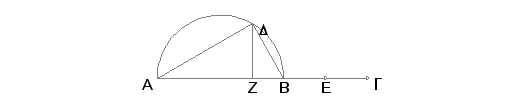
Uzmimo dve medijale AB i BG, samerljive samo u stepenu, i to takve da obuhvataju racionalan pravougaoniki da je kvadrat na AB veći od kvadrata na BG za kvadrat na duži nesamerljivoj sa AB, nacrtajmo na AB polukrug ADB, prepolovimo BG tačkom E i konstruišimo na AB paralelogram jednak kvadratu na BE sa dopunom u obliku kvadrata, naime paralelogram sa stranama AZ i ZB. Tada je AZ nesamerljivo po dužini sa ZB. Povicimo iz Z normalu ZD prema AB i spojimo D sa A i sa B.
Pošto je AZ nesamerljivo sa ZB, biće i pravougaonik sa stranama BA i AZ nesamerljiv sa pravougaonikom kome su starne AB, BZ. No pravougaonik sa stranama BA i AZ jednak je kvadratu na AD, a prljavougaonik sa staranama AB i BZ jednak je kvadratu na AB, pa je usled toga, kvadrat na AD nesamerljiv sa kvadratom na DB. I pošto je kvadrat na AB medijalan, biće medijalan i zbir kvadrata na AD i na DB. I pošto je BG udvostručeno DZ, biće pravougaonik sa stranama AB i BG dvaput veći od pravougaonika sa stranama AB i ZD. No pravougaonik sa stranama AB i BG je racionalan znači i pravougaonik sa stranama AB i ZD racionalan. A kako je pravougaonik sa stranama AB i ZD jednak pravougaoniku sa stranama AD i DB, biće i pravougaonik sa stranama AD i DB racionalan.
Na ovaj način su nađene dve takve duži AD i DB, nesamerljive u stepenu, da je površina satavljena od kvadrata na njima medijalna, a pravougaonik obuhvaćen tim dužima racionalan. A to je trebalo i dokazati.