35.

Naći dve duži nesamerljive u stepenu, takve da površina satavljena od kvadrata na njima bude medijalna i pravougaonik obuhvaćen tim dužima medijalan, i pri tome nesamerljiv sa površinom satavljenim od kvadrata na njima.

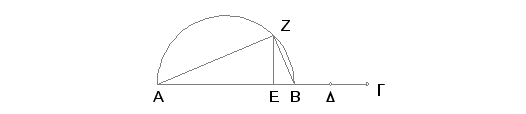
Uzmimo dve medijale AB i BG, samerljive samo u stepenu i tako da obuhvataju medijalan pravougaonik i da kvadrat na AB bude veći od kvadrata na BG za kvadrat na duži nesamerljivoj sa AB, nactajmo na AB polukrug ADB i učinimo i sve ostalo kao u prethodnom slučaju.
Pošto je AZ nesamerljivo po duži sa ZB, biće AD nesamerljivo sa DB u stepenu. I pošto je kvadrat na AB medijalan, biće medijalan i zbir kvadrata na AD i na DB. I pošto je pravougaonik sa stranama AZ i ZB jednak kvadratu na svakoj od duži BE i DE, biće BE jednako DZ: znači BG je udvostručena duž ZD, a pravougaonik sa stranama AB i BG dvaput veći od pravougaonika sa stranama AB i ZD. No pravougaonik sa stranama AB i BG je medijalan, pa je prema tome medijalan i pravougaonik sa stranama AD i DB. I pošto je AB nesamerljivo po dužini sa BG, a BG je samerljivo sa BE, biće AB nesamerljivo po dužini sa BE. Na taj način je kvadrat AB nesamerljiv sa pravougaonikom sa stranama AB i BE. No kvadrat na AB jednak je zbiru kvadrata na AD i na ZD, tj. pravougaoniku sa stranama AD i DB. Na ovaj način je nesamerljiva površina zbira kvadrata na AD i na DB sa površinom pravougaounika sa stranama AD i DB.
Na ovaj način su nađene duži AD i DB nesamerljive u stepenu, takve da površina sastavljena od kvadrata na njima bude medijalna, pravougaonik obuhvaćen tim dužima bude medijalan, i pri tome nesamerljiv sa površinom na njima.