36.

Ako se saberu dve racionalne duži, samerljive samo u stepenu, biće cela duž iracionalna: neka se zove binomijala.

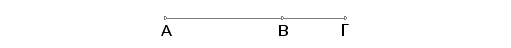
Saberimo dve racionalne duži AB i BG samerljive samo u stepenu. Tvrdim da je cela duž AG iracionalna.
Zaista, pošto je AB nesamerljiva sa BG po dužini, jer su one samerljive samo u stepenu, biće AB prema BG kao pravougaonik sa stranama AB i BG prema kvadratu na BG, pa je, prema tome, pravougaonik nesamerljiv sa kvadratom na BG. No sa pravougaonikom sa stranama AB i BG je samerljiv dvostruki pravougaonik sa stranama AB i BG, a sa kvadratom na BG samerljivi su kvadrati na AB i na BG zajedno, jer su AB i BG racionalne duži samerljive samo u stepenu. Prema tome je dvostruki pravougaonik sa stranama AB i BG nesamerljiv sa kvadratima na AB i na BG. I, posle sastavljanja, dvostruki pravougaonik sa stranama AB i BG sa zbirom kvadrata na AB i na BG, tj. kvadrat na AG je nesamerljiv sa površinom sastavljenom od kvadrata na AB i na BG. No površina sastavljena od kvadrata na AB i na BG je racionalna, te je prema tome kvadrat na AG iracionalan; znači duž AG je iracionalna. Neka se ona zove binomijala. A to je trebalo dokazati.