37.
Ako se saberu dve duži-medijale, samerljive samo u stepenu, koje obuhvataju racionalan pravougaonik, biće cela duž iracionalna. Neka se ona zove prva bimedijala.
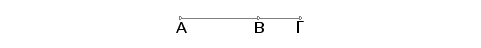
Saberimo dve medijale AB i BG, samerljive samo u stepenu, koje obuhvataju racionalan pravougaonik. Tvrdim da je cela duž AG iracionalna.
Zaista, pošto je AB nesamerljiva sa BG po dužini biće i zbir kvadrata na AB i BG nesamerljiv sa udvostručenim pravougaonikom sa stranama AB i BG. I posle sastavljanja kvadrata na AB i na BG sa udvostručenim pravougaonikom sa stranama AB i BG, a to je baš kvadrat na AG, biće taj kvadrat nesamerljiv sa pravougaonikom sa stranama AB i BG. No pravougaonik sa stranama AB i BG je racionalan, jer se predpostavlja da AB i BG obuhvataju racionalan pravougaonik. Znači kvadrat na AG je iracionalan, te je, prema tome, i duž AG iracionalna. Neka se ona zove prva bimedijala. A to je trebalo dokazati.