40.
Ako se saberu dve duži, nesamerljive u stepenu, za koje je zbir kvadrata na njima medijalan, apravougaonik obuhvaćen njima racionalan,biće cela duž iracionalna. Neka se ona zove "strana kvadrata jednakog zbiru racionalne i medijalne površine".
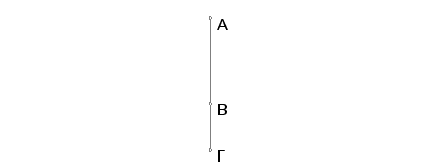
Neka se saberu dve duži AB i BG, nesamerljive u stepenu, pod navedenim uslovima. Tvrdim da je duž AG iracionalana.
Zaista, pošto je površina sastavljena od kvadrata na AB i na BG medijalna, a udvostručen pravougaonik sa stranama AB i BG je racionalan, biće zbir kvadrata na AB i na BG nesamerljiv sa udvostručenim pravougaonikom sa stranama AB i BG. Pa će kvadrat na AG biti nesamerljiv sa udvostručenim pravougaonikom kome su strane AB i BG. No udvostručeni pravougaonik sa stranama AB i BG je racionalan, pa je kvadrat na AG iracionalan. Dakle, i duž AG je iracionalna. Neka se ona zove "strana kvadrata jednakog zbiru racionalne i medijalne površine". A to je trebalo dokazati.