41.
Ako se saberu dve duži, nesamerljive u stepene, za koje je zbir kvadrata na njima medijalan i pravougaonik obuhvaćen njima medijalan, i pri tome je pravougaonik nesamerljiv sa zbirom kvadrata,biće cela duž iracionalna. Neka se ona zove "strana kvadrata jednakog zbiru dve medijalne površine".
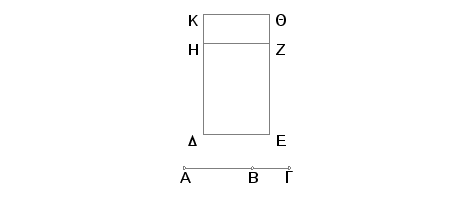
Saberimo dve duži AB i BG, nesamerljive u stepenu, pod navedenim uslovima. Tvrdim da je duž AG iracionalna.
Zaista, uzmimo racionalnu duž DE i konstruišimo na DE pravougaonik DZ, jednak zbiru kvadrata na AB i na BG, a pravougaonik HQ jednak udvostručenom pravougaoniku sa stranama AB i BG. Ceo pravougaonik DQ je tada jednak kvadratu na AG. Pošto je površina jednaka zbiru kvadrata na AB i na BG medijalna i jednaka pravougaoniku DZ, biće, prema tome, i pravougaonik DZ medijalan. A on je konstruisan na racionalnoj duži DE, te je, prema tome, racionalna i duž DH i nesamerljiva po dužini sa DE. Iz istih razloga je racionalna i duž HK i nesamerljiva po dužini sa HZ, tj. sa DE. A pošto je zbir kvadrata na AB i na BG nesamerljiv sa udvostručenim pravougaonikom kome su strane AB i BG, biće nesamerljiv i pravougaonik DZ sa pravougaonikom HQ. Prema tome je nesamerljiva i duž DH sa HK. No one su racionalne. Prema tome su DH i HK racionalne i samerljive samo u stepenu. Na ovaj načžin je DK iracionalna i takozvana binomijala. No DE je racionalna, pa je, prema tome, DQ iracionalan pravougaonik i strana jednakog mu kvadrata takođe iracionalna. Ali strana kvadrata jednakog pravougaoniku QD je duž AG. Prema tome je iracionalna i duž AG. Neka se zove "strana kvadrata jednakog zbiru dve medijalne površine". A to je trebalo dokazati.