44.
Druga medijala se deli samo jednom tačkom.
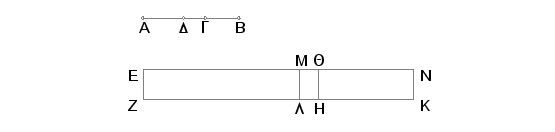
Neka je AB druga bimedijala, podeljena tačkom G tako da AG i GB budu medijale samerljive samo u stepenu i da obuhvataju medijalan pravougaonik. Pri tome je jasno da G nije sredina, jer delovi nisu samerljivi po dužini. Tvrdim da se AB ne deli drugom tačkom.
Zaista, ako je to moguće, neka se deli i drugom tačkom D i to tako da AG nije isto što i DB i da je AG, po pretpostavci, veće. Očevidno je, kako smo ranije dokazali, da je zbir kvadrata na AD i na DB manji od zbira kvadrata na AG i na GB, i da su AD i DB medijale, samerljive samo u stepenu, koje obuhvataju medijalan pravougaonik. Uzmimo racionalnu duž EZ i konstruišimo na EZ pravougli paralelogram EK jednak kvadratu na AB, i oduzmimo pravougaonik EH jednak zbiru kvadrata na AG i na GB. Tada je ostatak QK jednak dvostrukom pravougaoniku sa stranama AG i GB. Zatim oduzmimo pravougaonik EA jednak zbiru kvadrata na AD i na DB, koji je, kako smo dokazali, manji od zbira kvadrata na AG i GB. Tada je i ostatak MK jednak dvostrukom pravougaoniku sa stranama AD i DB. I pošto su kvadrati na AG i na GB medijalni, biće medijalan i pravougaonik EH. I on se konstruiše na racionalnoj duži EZ, znači da je racionalna i duž EQ i nesamerljiva po dužini sa EZ. Iz istih razloga je i duž QN racionalna i nesamerljiva po dužini sa EZ. I pošto su AG i GB medijale, samerljive samo po dužini, biće AG nesamerljivo po dužini sa GB. No AG je prema GB kao kvadrat na AG prema pravougaoniku sa stranama AG i GB. Pa prema tome je kvadrat na AG nesamerljiv sa pravougaonikom kome su strane AG i GB. Znači kvadrat na AG je samerljiv sa zbirom kvadrata na AG i na GB, jer su AG i GB samerljive u stepenu. No dvostruki pravoukaonik sa stranama AG i GB je samerljiv sa pravougaonikom kome su stane AG i GB. Prema tome je zbir kvadrata na AG i na GB nesamerljiv sa dvostrukim pravougaonkom kome su strane AG i GB. No zbir kvadrata na AG i na GB jednak je pravougaoniku EH, a dvostrukom pravougaoniku sa stranama AG i GB jednak je pravougaoniku QK. Prema tome je EH nesamerljivo sa QK, pa i EQ nesamerljivo po dužini sa QN. A one su racionalne. Na ovaj način su EQ i QN su racionalne duži samerljive samo u stepenu. Ali, ako se saberu dve racionalne duži samerljive samo u stepenu, biće celina (zbir) iracionalna, takozvana binomijala. Prema tome je EN binomijala koja se deli tačkom Q. Na isti način se dokazuje da su i EM, MN racionalne duži samerljive samo u stepenu. I EN je binomijala, koja se deli i u jednoj i u drugoj tački, naime u Q i u M, a pri tome EQ nije isto što je MN, pošto je zbir kvadrata na AG i na GB veći od zbira kvadrata na AD i na DB. No zbir kvadrata na AD i na DB je veći od dvostrukog pravougaonika sa stranama AD i DB. U toliko pre je i zbir kvadrata na AG i na GB, tj. pravougaonik EH, veći od dvostrukog pravougaonika sa stranama AD i DB, tj. pravougaonika MK. Znači EQ je veći od MN. I prema tome EQ neće biti isto što i MN. A to je trebalo dokazati.