49.

Naći drugu binomijalu.

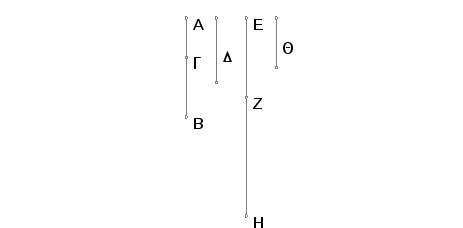
Uzmimo dva broja AG i GB i to tako da je razmera njihovog zbira AB prema BG kao kvadratnog broja prema kvadratnom broju a da razmera prema AG nije kao kvadrtnom broju, i neka bude data racionalna duž D i neka je EZ samerljivo po dužini sa D. Na ovaj način i EZ je racionalno. I uradimo tako da se broj GA odnosi prema broju AB kao kvadrat na EZ prema kvadratu na ZH. Tada je kvadrat na EZ samerljiv sa kvadratom na ZH. Znači i ZH je racionalno. I pošto broj GA ne stoji prema broju AB u razmeri kvadratnog broja prema kvadratnom broju, neće biti ni kvadrat na EZ prema kvadratu na ZH u razmeri kvadratnog broja prema kvadratnom broju. Znači EZ je nesamerljivo po dužini sa ZH. Na ovaj način su duži EZ i ZH racionalne, ali samerljive samo u stepenu. Dakle, EH je binomijala.
Treba dokazati da je druga.
Zaista, pošto se, obrnuto, broj BA odnosi prema broju AG kao kvadrat na HZ prema kvadratu na ZE, a BA je veće od AG, biće ikvadrat na HZ veći od kvadrata na ZE. Neka sad kvadrat na HZ bude jednak zbiru kvadrata na EZ i na Q. Na ovaj način, posle permutovanja, AB je prema BG kao kvadrat na ZH prema kvadratu na Q. Ali AB je u razmeri prema BG kao kvadratni broj prema kvadratnom broju. Prema tome i kvadrat na ZH stoji u razmeri prema kvadratu na Q kao kvadratni broj prema kvadratnom broju. Na ovaj način ZH je samerljivo po dužini sa Q. I prema tome je kvadrat na ZH veći od kvadrata na ZE za kvadrat na duži koja je samerljiva sa većim delom. Duži ZH i ZE su racionalne i samerljive po dužini sa D.
Na ovaj način EH je druga binomijala. A to je trebalo dokazati.