51.
Naći četvrtu binomijalu.
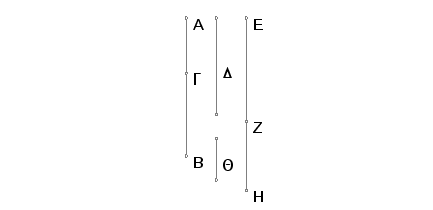
Uzmimo dva broja AG i GB i to tako da razmera AB ni prema BG ni prema AG nije razmera kvadratnog broja prema kvadratnom broju, i neka bude data racionalna duž D i neka je EZ samerljiva po dužini sa D. Na taj način je i EZ racionalno. I uradimo tako da se broj BA tako odnosi prema broju AG kao kvadrat na EZ prema kvadratu na ZH. Tada je kvadrat na EZ samerljiv sa kvadratnom na ZH. Znači i ZH je racionalno. I pošto broj BA ne stoji prema AG u razmeri kvadratnog broja prema kvadratnom broju, neće biti ni kvadrat na EZ prema kvadratu na ZH u razmeri kvadratnog broja prema kvadratnom broju. I znači EZ je nesamerljivo po dužini sa ZH. Na ovaj način su EZ i ZH racionalne, ali samerljive samo u stepenu. Znači EZ je binomijala.
Tvrdim da je četvrta.
Zaista, pošto je BA prema AG kao kvadrat na EZ prema kvadratu na ZH (BA je veće od AG), kvadrat na EZ je veći od kvadrata na ZH. Neka je sad kvadrat na EZ jednak zbiru kvadrata na ZH i na Q. Na ovaj način posle permutovanja, broj AB je prema BG kao kvadrat na EZ prema kvadratu na Q. Ali AB nije u razmeri prema BG kao kvadratni broj prema kvadratnom broju, neće biti ni kvadrat na EZ prema kvadratu na Q u razmeri kvadratnog broja prema kvadratnom broju. Pa znači EZ je nesamerljivo po dužini sa Q. I prema tome je kvadrat na EZ veći od kvadrata na HZ za kvadrat na duži koja je nesamerljiva sa većim delom. Duži EZ i ZH su racionalne i samerljive samo u stepnu, i EZ je samerljivo po dužini sa D.
Na ovaj način, EH je četvrta binomijala. A to je trebalo dokazati.