Lema
Neka su AB i BG dva kvadrata. Postavimo ih tako da DB i BE budu u istoj pravoj. Biće tada i ZB u istoj pravoj sa BH. Pa dopunimo paralelogram AG. Tvrdim da je AG kvadrat, i da je pravougaonik DH srednja proporcionala za kvadrate AB i BG i pravougaonik DG srednja proporcionala za kvadrate AG i GB.
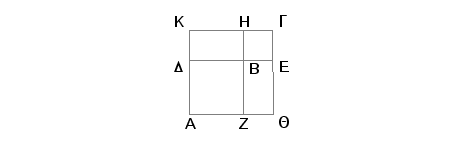
Zaista, pošto je DB jednaka BZ i BE jednaka BH, biće i cela DE jednaka celoj ZH. No DE jedanko je svakoj od AQ i KG, a ZH jednako svakoj od AK i QG. Znači svaka od AQ i KG jednaka svakoj od AK i QG. Prema tome je AG jednakostrani paralelogram, a on je i pravougli. Znači AG je kvadrat.
Pošto je ZB prema BH kao DB prema BE, ali ZB je prema BH kao AB prema DH kao DH prema BG. Znači DH je srednja proporcionala za AB i BG.
Tvrdim još da je i DG srednja proporcionala za AG i BG.
Zaista, pošto je AD prema DK kao KH prema HG, jer je svaka jednaka svakoj, biće, posle dodavanja, AK prema KD kao KG prema GH, ali AK je prema KD kao AG prema GD, a KG je prema GH kao DG prema GB, i na taj način, je AG prema DG kao DG prema BG. Znači DG je srednja proporcionala za AG i GB. A to je trebalo i dokazati.