54.

Ako su racionalna duž i prva bionomijala strane nekog pravougaonika biće strana kvadrata sa površinom jednakom tom pravougaoniku iracionalna, i to binomijala.

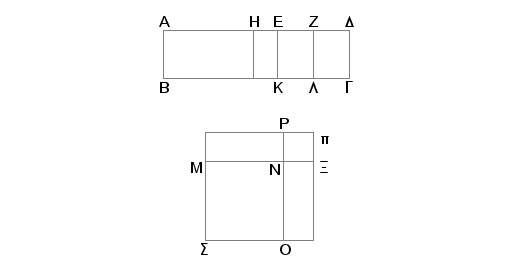
Neka je površina AG obuhvaćena racionalnom duži AB i prvom binomijalom AD. Tvrdim da je strana kvadrata sa površinom jednakom AG iracionalna, i to binomijala.
Zaista, pošto je AD prva binomijala, podelimo je tačkom E na dva racionalna dela i neka AE bude veći deo. Jasno je da su AE i ED racionalne i samerljive samo u stepenu i da je kvadrat na AE veći od vkadrata na ED za vkadrat na duži koja je samerljiva po dužini sa AE i da je AE samerljivo po dužini sa AB koju smo izabrali kao racionalnu.
Prepolovimo ED tačkom Z. I pošto je kvadrat na AE veći od kvadrata na ED za kvadrat na duži koja je samerljiva po dužini sa AE, onda, ako se na većoj AE konstruiši pravougaonik, sa kvadratnom dopunom, jednak četvrtini kvadrata na manjoj, tj. kvadratu na EZ, taj pravougaonik će deliti duž AE na delove samerljive sa njom. Konstruišimo sad na AE pravougaonik jednak kvadratu na EZ sa stranama jednakim AH i HE. Biće tada AH samerljivo po dužini sa EH. I povucimo iz tačaka H, E, Z paralelno svakoj od AB i GD prave HQ, EK, ZL. Dalje, konstruišimo kvadrat SN jednak pravougaoniku AQ i kvadrat Np jednak pravougaoniku HK i to tako da strane MN i NX budu na istoj pravoj. Tada su na istoj pravoj i strane PN i NO. I dopunimo paralelogram Sp. Biće tada Sp kvadrat. I pošto je pravougaonik sa stranama AH i HE jednak kvadratu na EZ, onda je AH prema EZ kao ZE prema EH. I na taj način AQ je prema EL kao EL prema KH. Prema tome je EL srednja proporcionala za AQ i HK. Ali AQ je jednako SN, a HK jednako Np. Zbog toga je EL srednja proporcionala za SN i Np. Ali srednja proporcionala za SN i Np je takođe i MP. Na ovaj način je EL jednako MP, a jednako i OX. Jednak je zbir AQ i HK zbiru SN i Np. Dakle celo AG jednako je celom Sp, tj. kvadratu na MX. Znači MX je strana kvadrata jednakog površini AG.
Tvrdim da je MX binomijala.
Zaista, pošto je AH samerljivo sa HE, biće AE samerljivo sa svakim od AH i HE. A pretpostavljeno je da je i AE samerljivo sa AB. Prema tome AH i HE su samerljivi sa AB. A kako je AB racionalno, biće racionalno i svako od AH i HE, a racionalno je i svako od AQ i HK, i AQ je samerljivo sa HK. Ali AQ je jednako SN, a HK - Np, pa su prema tome, SN i Np, tj. kvadrat na MN i kvadrat na NX, racionalni i samerljivi. I pošto je AE nesamerljivo po dužini sa ED, ali AE je samerljivo sa AH i DE samerljivo sa EZ, biće AH samerljivo sa EZ, pa znači i AQ nesamerljivo sa EL. Ali je AQ jednako SN, a EL jednako MP, pa je zbog toga i SN nesamerljivo sa MP. No SN je prema MP kao ON prema NP. Znači i ON je nesamerljivo sa NP. Ali ON je jednako MN i Np jednako NX pa prema tome je i MN nesamerljivo s NX. I kvadrat na MN je samerljiv sa kvadratom na NX, i svaki je racionalan. Znači MN i MX su racionalni i samerljivi samo u stepenu.
Na ovaj način je MX binomijala i jednaka strani kvadrata jednakog površini AG. A to je trebalo dokazati.