58.

Ako su racionalna duž i peta binomijala strane nekog pravougaonika, biće strana kvadrata sa površinom jednakom tom pravougaoniku takozvana strana kvadrata jednakog zbiru racionalne i medijalne površine.

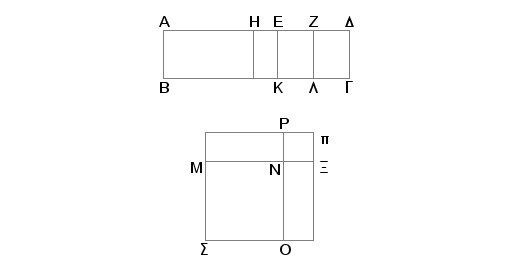
Neka je površina AG obuhvaćena racionalnom duž AB i petom binomijalom AD, podeljenom na delove tačkom E, pri čemu je veći deo AE. Tvrdim, da je strana kvadrata sa površinom jednakom AG iracionalna i takozvana strana kvadrata jednakog zbiru racionalne i medijalne površine.
Zaista, izvršimo iste konstrukcije kao i ranije. Jasno je da je MX strana kvadrata sa površinom jednakom AG. Treba dokazati da je to "strana kvadrata jednakog zbiru racionalne i medijalne površine". Zaista, pošto je AH, nesamerljivo sa HE, biće i AQ nesamerljivo sa QE, tj. kvadrat na MN sa kvadratom na NX, a MN i NX biće duži nesamerljive u stepenu. A pošto je AD peta binomijala i njen manji deo je ED, biće ED samerljivo po dužini sa AB. No AE je nesamerljivo sa ED. Prema tome je i AB nesamerljivo po dužini sa AE [BA i AE su racionalne i samerljive samo u stepenu]. Znači površina AK, zbir kvadrata na MN i NX, medijalna je. I pošto je DE samerljivo po dužini sa AB, tj. sa EK, a DE je samerljivo sa EZ, biće i EZ samerljivo sa EK, a EK i racionalno. Prema tome je racionalna i površina EL, tj. MP, tj. površina sa stranama MN i NX. Na ovaj način su MN i NX nesamerljive u stepenu, zbir kvadrata na njima medijalan, a pravougaonik obuhvaćen njima racionalan.
Na ovaj način duž MX je strana kvadrata jednakog zbiru racionalne i medijalne površine i strana kvadrat jednakog površini AG. A to je trebalo dokazati.