59.

Ako su racionalan duž i šesta binomijala strane nekog pravougaonika, biće strana kvadrata sa površinom jednakom tom pravougaoniku takozvana strana kvadrat jednakog zbiru dve medijalne površine.

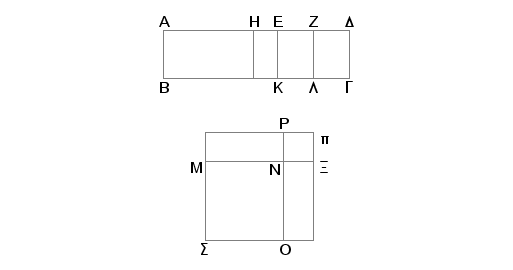
Neka je površina ABGD obuhvaćena racionalnom duži AB i šestom binomijalom AD podeljenom na delove tačkom E, pri čemu je veći deo AE. Tvrdim da je strana kvadrata sa površinom jednakom AG takozvana strana kvadrat jednakog zbiru dve medijalne površine.
Zaista, izvršimo iste konstrukcije kao i ranije. Tada je jasno da je MX strana kvadrat sa površinom jednakom AG i da su MN i NX nesamerljive u stepenu. I pošto je EA nesamerljiva po dužini sa AB, biće EA i AB racionalne i nesamerljive samo u stepenu. Prema tome je medijalna površina AK, zbir kvadrata na MN i na NX, Dalje, pošto je ED nesamerljiva po dužini sa AB, biće nesamerljiva i duž ZE sa EK. Na taj način su ZE i EK racionalne i samerljive samo u stepenu. Prema tome je površina EL medijalna, a to znači da je medijalna i površina MP, pravougaonika sa stranama MN i NX. A pošto je AE nesamerljivo sa EZ, biće nesamerljiva i površina AK sa površinom EL. No AK je zbir kvadrat na MN i na NX, a EL je pravougaonik sa stranama MN i NX. Prema tome su nesamerljivi zbir kvadrata na MN i na NX i pravougaonik sa stranama MN i NX. I svaki od njih je medijalan. I duži MN i NX su nesamerljive u stepenu.
Na ovaj način, MX je strana kvadrata jednakog zbiru dve medijalne površine i strana kvadrata jednakog površini AG. A to je trebalo dokazati.