Lema
Ako je neka duž podeljena na nejednake delove, zbir kvadrata na tim delovima je veći od dvostrukog pravougaonika obuhvaćenog tim nejednakim delovima.
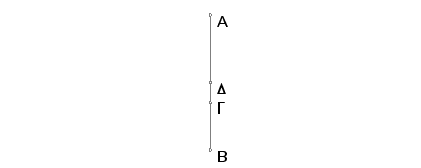
Neka je AB duž podeljena na nejednake delove tačkom G i neka je AG veći deo. Tvrdim da je zbir kvadrata na AG i na GB veći od dvostrukog pravougaonika kome su AG i GB strane.
Prepolovimo AB tačkom D na jednake delvoe, a tačkom G na nejednake, biće pravougaonik sa stranama AG i GB sa kvadratom na GD jednak kvadratu na AD. Prema tome je pravougaonik sa stranama AG i GB manji od kvadrata na AD. Pa znači i dvostruki taj isti pravougaonik je manji od udvostručenog kvadrata na AD. No zbir kvadrata na AG i na GB jednak je udvostručenom zbiru kvadrata na AD i na DG. Na ovaj način zbir kvadrata na AG i na GB je veći od dvostukog pravougaonika sa stranama AG i GB. A to je trebalo dokazati.