60.
Ako pravougaonik, konstruisan na racionalnoj duži, ima površinu jednaku površini kvadrata na binomijali, njegova širina je prva binomijala.
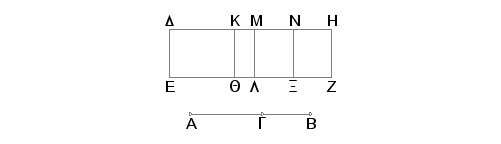
Neka je AB binomijala podeljena tačkom G tako da je veći deo AG. odmerimo racionalnu duž DE i konstruišimo na DE paralelogram DEZH, kome je širina DH, jednak kvadratu na AB. Tvrdim, da je DH prva binomijala.
Zaista, konstruišimo na DE pravougaonik DQ jednak kvadratu na AG i pravougaonik KL jednak kvadratu na BG.
Tada je sotatak MZ jednak dvostrukoj površini pravougaonika sa stranama AG i GB. Prepolovimo MH tačkom N i neka je NX paralelna svakoj od ML i HZ. Tada je svaka od površine MX i NZ jednaka jedanput uzetom pravougaoniku sa stranama AG i GB. I pošto je AB binomijala podeljena tačkom G, biće AG i GB racioanlne samerljive samo u stepenu. Prema tome su i kvadrati na AG i na GB racionalni i samerljivi među sobom. Na taj način i zbir kvadrata na AG i na GB je samerljiv sa kvadratima na AG i na GB, pa je, znači, zbir kvadrata na AG i na GB racionalan. I jednak je taj zbir pravougaoniku DA. Prema tome je racionalan i pravougaonik DL. A isti je konstruisan na racionalnoj duži DE, zbog toga je racionalan i DM i samerljiva po dužini sa DE. Zatim, pošto su AG i GB racionalne i samerljive samo u stepenu, biće dvaput uzeti pravougaonik sa stranama AG i GB, tj. pravouganok MZ, medijalan. I on se konstruiše na racionalnoj duži ML, znači da je racionalan i duž MH i nesamerljiva po dužini sa ML, tj. sa DE. A i MD je racionalan i samerljiva po dužini sa DE. Zbog toga je DM nesamerljiva po dužini sa MH. A one su racionalne. Na ovaj način, DM i MH su racionalne, samerljive samo u stepenu, i DH je, stoga, binomijala.
Treba dokazati da je prva.
Pošto je za kvadrat na AG i na GB srednja proporcionala pravougaonik kome su tstrane AG i GB, biće i za DQ i KA srednja proporcionala MX No DQ je prema MX kao MX prema KL, tj. DK je prema MN kao MN prema MK. Znači pravougaonik sa stranama DK i KM jednak je kvadratu na MN. I pošto je kvadrat na AG samerljiv sa kvadratom na GB, biće samerljiva i površina DQ sa površinom KL. Tada je i duž DK samerljiva sa KM. I pošto je zbir kvadrata na AG i na GB, veći od dvostrukog pravougaonika kome su strane AG i GB, biće i DL veće od MZ. Zbog toga je i duž DM veća od MH. I pravougaonik sa stranama DK i KM jednak je kvadratu na MN, tj. četvrtini kvadrata na MH, i DK je samerljivo sa KM. No postoje dve nejednake duži i na većoj je konstruisan paralelogram sa kvadratnom dopunom jednakom četvrtini kvadrata, na manjoj i ako je on se deli na samerljive delvoe, biće kvadrat na većoj duži veći odkvadrata na manjoj za kvadrat na duži, koja je samerljiva sa većom. Na ovaj način, kvadrat na DM je veći od kvadrata na manjoj MH za kvadrat na duži samerljivoj sa DM. I DM i MH su racionalne duži i DM, veći deo, biće samerljiv po dužini sa duži DE, uzetoj za racionalnu.
Na ovaj način DH je prva binomijala. A to je trabalo dokazati.