62.
Ako pravougaonik, konstruisan na racionalnoj duži, ima površinu jednaku površini kvadrata na drugoj bimedijali, njegova širina je treća binomijala.
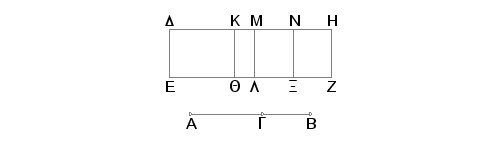
Neka je AB druga bimedijala podeljena tačkom G na dve medijale tako da je veća AG. Odmerimo racionalnu duž DE i konstruišimo na DE paralelogram DZ, kome je širina DH, jednak kvadratu na AB. Tvrdim da je DH treća binomijala.
Zaista, izvršimo iste konstrukcije kao i ranije. I pošto je AB druga bimedijala podeljena tačkom G, biće AG i GB dve medijale, samerljive samo u stepenu, koje obuhvataju medijalan pravougaonik. Prema tome je medijalan i zbir kvadrata na AG i na GB, i jednak je površini DL. Znači i ova površina je medijalan. A konstruisana je na racionalnoj duži DE. Prema tome je racionalna i duž MD i nesamerljiva po dužini sa DE. Iz istih razloga racionalna je i duž MH i nesamerljiva pod užini sa ML, tj. sa DE. Znači racionalan je svaka od duži DM i MH i nesamerljiva po dužini sa DE. I pošto je AG nesamerljivo po dužini sa GB, a AG je prema GB kao kvadrat na AG prema pravougaoniku sa stranama AG i GB, biće nesamerljiv i kvadrat na AG sa pravougaonikom kome su strane AG i GB. Prema tome i zbir kvadrata na AG i na GB je nesamerljiv sa dvostrukim pravougaonikom na AG i na GB, tj. površina DL sa površinom MZ. A tada su nesamerljive i duži DM i MH. A one su racionalne, Na ovaj način, DH je binomijala.
Treba dokazati da je treća.
Slično prethodnom zaključujemo da je DM veća od MH, da je DK samerljiva sa KM, i da je površina pravougaonika sa stranama DK i KM jednaka kvadratu na MN. Znači, kvadrat na DM je veći od kvadrata na MH za vkadrat na duži koja je samerljiva sa DM. I nijedna od DM i MH neće biti samerljiva po dužini sa DE.
Na ovaj način, DH je treća binomijala. A to je trebalo dokazati.