63.
Ako pravougaoniku, konstruisan na racionalnoj duži, ima površinu jednaku površini kvadrata na većoj bimedijali, njegova širina je četvrta binomijala.
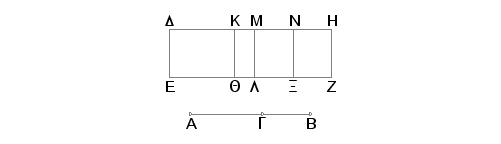
Neka je AB "veća" podeljena tačkom G tako da je AG veći deo od GB, da je DE racionalna i da paralelogram DZ jednak kvadratu na AB, konstruisan na DE, ima širinu DH. Tvrdim da je DH četvrta binomijala.
Zaista, izvršimo iste konstrukcije kao i ranije. I pošto je AB "veća" podeljena tačkom G, biće AG i GB nesamerljive u stepenu, zbir kvadrata na njima racionalan, a pravougaonik sa takvim stranama medijalan. Pošto je sad zbir kvadrata na AG i na GB racionalan, zbog toga je racionalna i površina DL, a usled toga je racionalna i duž DM i samerljiva po dužini sa DE. Zatim, pošto je medijalan dvostruki pravougaonik sa stranama AG i GB, tj. površina MZ, a konstruisan je na racionalnoj duži ML, biće racionalan i MH i nesamerljiva po dužini sa DE. A i DM je nesamerljiva po dužini sa MH. Prema tome su DM i MH racionalne samerljive samo u stepenu. Na ovaj način je DH binomijala.
Treba dokazati da je četvrta.
Slično prethodnom se dokazuje da je DM veće od MH i da je pravougaonik sa stranama DK i KM jednak kvadratu na MN. I pošto je sad kvadrat na AG nesamerljiv sa kvadratom na GB, biće i površina DQ nesamerljiva sa KL. Zbog toga je i duž DK nesamerljiva sa KM. No ako postoje dve nejednake duži i ako je na većoj konstuisan sa kvadratnom dopunom paralelogram, koji je jednak četvrtini kvadrata na manjoj, i deli tu duž na delove nesamerljive po dužini, biće kvadrat na većoj duži veći od kvadrata na manjoj za kvadrat na duži koja je nesamerljiva po dužini sa većom duži. Prema tome je kvadrat na DM veći od kvadrata na MH za kvadrat na duži koja je nesamerljiva sa DM. I duži DM i MH su racionalne i samerljive samo u stepenu. I DM je samerljiva sa izabranom racionalnom duži DE.
Na ovaj način DH je četvrta binomijala. A to je trebalo dokazati.