64.
Ako pravougaonik, konstruisan na racionalnoj duži, ima površinu jednaku kvadratu na strani kvadrata jednakog zbiru racionalne i medijalne površine, njegova širina je peta binomijala.
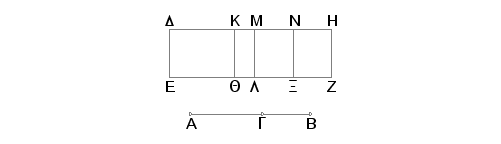
Neka je AB strana kvadrata jednakog zbiru racionalne i medijalne površine, podeljena tačkom G na duži i neka je AG veća duž, i odmerena je racionalna duž DE, i neka paralelogram DZ, jednak kvadratu na AB, konstruisan na DE, ima širinu DH. Tvrdim da je DH peta binomijala.
Izvršimo iste konstukcije kao i ranije. Pošto je sada AB "strana kvadrata jednakog zbiru racionalne i medijalne površine", podeljena tačkom G, biće AG i GB nesamerljive u stepenu, ali zbir kvadrata na njima medijalan, a pravougaonik sa takvim stranama racionalan. Pošti je sada zbir kvadrata na AG i na GB medijalan, biće medijalna i površina DA. Prema tome je DM racionalna i nesamerljiva po dužini sa DE. Zatim pošto je dvostruki pravougaonik sa stranama AG i GB, tj. površina MZ racionalna, racionalana je i duž MH i nesamerljiva sa DE. Prema tome DM je nesamerljiva sa MH. Na ovaj način, duž DM i MH su racionalne, samerljive samo u stepenu. A to znači da je DH binomijala.
Tvrdim da je peta.
Zaista, slično se dokazuje da je pravougaonik sa stranama DK i KM jednak kvadratu na MN,i da je D K nesamerljiva po dužini sa KM. Znači kvadrat DM je veći od kvadrata na MH za kvadrat na duži, koja je nesamerljiva sa DM. I duži DM i MH (racionalne) samerljive su samo u stepenu i manja, MH, samerljiva je po dužini sa DE.
Na ovaj način, DH je peta binomijala. A to je trebalo i dokazati.