67.

Duž samerljiva po dužini sa bimedijalom i same je bimedijala i to istog reda.

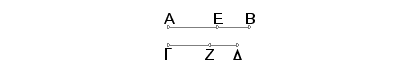
Neka je AB bimedijala i neka je duž DG samerljiva sa AB. Tvrdim, da je GD bimedijala i to istog reda kao i AB.
Zaista, pošto je AB bimedijala podelimo je tačkom E na medijale. Tada su AE i EB medijale samerljive samo ui stepenima. Uradimo tako da AB bude prema GD kao AE prema GZ. Tada je ostatak EB prema ostatku ZD kao AB prema GD. No AB je samerljiva po dužini sa GD. Zbog toga je svaka od AE i EB samerljiva sa svakom GZ i ZD. No AE i EB su medijale pa prema tome su medijale i GZ i ZD. I pošto je AE prema EB kao GZ prema ZD, a AE i EB su samerljive samo u stepenu, biće GZ i ZD samerljive samo u stepenu. A dokazano je da su one medijale. Na ovaj način GD je medijala.
Tvrdim da je ona istog reda kao i AB.
Zaista, pošto je AE prema EB kao GZ prema ZD i prema tome je kvadrat na AE prema pravougaoniku sa stranama AE i EB kao kvadrat na GZ prema pravougaoniku sa stranama GZ i ZD, onda posle permutovanja kvadrat na AE biće prema kvadratu na GZ kao pravougaonik sa AE i EB prema pravougaoniku sa GZ i ZD. No kvadrat na AE je samerljiv sa kvdartom na GZ, pa zbog toga je i pravougaonik sa AE i EB samerljiv sa pravougaonukom GZ i ZD. Ako je sada pravougaonik sa AE i EB racionalan biće racionalan i pravougaonik sa GZ i ZD (i usled toga je prva bimedijala). A ako je medijalan prvi biće medijalan i drugi i to oba drugog reda.
I usled toga GD biće istog reda kao i AB. A to je trebalo i dokazati.