68.

Duž samerljiva sa većom biće i sama veća.

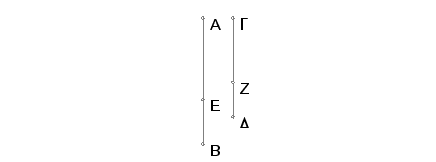
Neka je AB veća i GD je samerljiva sa AB. Tvrdim, da je i G veća.
Podelimo AB tačkom E. Tada su AE i EB nesamerljive u stepenu i zbir kvadrata na njima je racionalan, a pravougaonik od njim medijalan. I uradimo ono isto što i ranije. I pošto je AB prema GD kao AE prema GZ i kao EB prema ZD, i na taj način kako je AE prema GZ tako je i EB prema ZD. No AB je samerljivo sa GD, pa je i svaka od AE i EB samerljiva je sa svakom od GZ i ZD. I pošto je AE prema GZ kao GZ prema ZD, znači, posle sabiranja, AB je prema BE kao GD prema DZ. Prema tome i kvadrat na AB je prema kvadratu na BE kao kvadrat na GD prema kvadratu na DZ. Na sličan način se dokazuje da kako se kvadrat na AB odnosi prema kvadratu na AE tako se i kvadrat na GZ. Dakle, kvadrat na AB je premazbiru kvadrat na AE i na EB kao kvadrat na GD prema zbiru kvadrata na GZ i na ZD. I na taj način, posle permutovanja, kvadrat na AB je prema kvadratu na GD kao zbir kvadrata na AE i na EB prema zbiru kvadrata na GZ i na ZD. No kvadrat na AB je samerljiv sa kvadartom na GD, pa prema tome je smerljiv i zbir kvadrata na AE i na EB sa zbirom kvadrata na GZ i na ZD. A zbir kvadrata na AE i na EB je racionalan, znači i zbir kvadrata na GZ i ZD je racionalan. Na sličan način i dvostruki pravougaonik sa stranama AE i EB je samerljiv sa dvostrukim pravougaonikom sa stranama GZ i ZD. A kako je dvostruki pravougaonik sa AE i EB medijalan, biće medijalan i dvostruki pravougaonik sa GZ i ZD. Na ovaj način GZ i ZD, nesamerljive u stepenu daju zbir kvadrata na njima racionalan, a dvostruki pravougaonik obuhvaćen njima medijalan. Cela duž GD je prema tome iracionalna, takozvana "veća".
Na ovaj način, duž samerljiva sa "većom" i sama je "veća". A to je trebalo dokazati.