70.
Duž samerljiva sa "stranom kvadrata jednakog zbiru dve medijalne površine" i sama je sa "strana kvadrata jednakog zbiru dve medijalne površine".
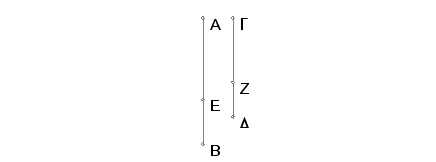
Neka je AB "strana kvadrata jednakog zbiru dve medijalne površine" i GD je duž samerljiva sa AB. Treba dokazati da je i GD "strana kvadrata jednakog zbiru dve medijalne površine".
Zaista, pošto je AB "strana kvadrata jednakog zbiru dve medijalne površine", podelimo je tačkom E na duži. Tada su AE i EB nesamerljive u stepenu i zbir kvadrata na njima medijalan i pravougaonik sa takvim stranama medijala i taj zbir kvadrata na AE i na EB nesamerljiv sa pravougaonikom kome su strane AE i EB. Izvršimo iste konstrukcije kao i ranije. Slično se dokazuje da su i GZ i ZD nesamerljive u stepenu i da je nesamerljiv zbir kvadrata na AE i na EB sa zbirom kvadrata na GZ i na ZD, a takođe da je pravougaonik sa stranama AE i EB samerljiv sa pravougaonikom sa stranama GZ i ZD. I prema tome je zbir kvadrata na GZ i na ZD medijalan i pravougaonik sa stranama GZ i ZD medijalan i zbir kvadarata na GZ i na ZD nesamerljiv sa pravougaonikom sa stranama GZ i ZD.
Na ovaj način GD je "strana kvadrata jednakog zbiru dve medijalne površine". A to je trebalo dokazati.