71.

Pri sabiranju racionalnog i medijalnog (racionalne i medijalne površine) mogu se dobiti četiri iracionalnosti: ili binomijala, ili prva bimedijala, ili "veća", ili "strana kvadrata jednakog zbiru dve racionalne i medijalne površine".

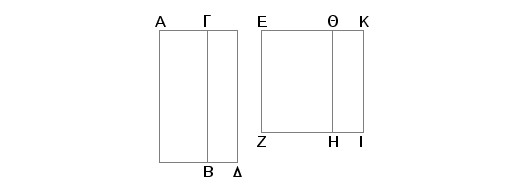
Neka je AB racionalna površina, a GD - medijalna. Tvrdim da strana kvadrata jednakog površini AD može biti: ili binomijala, ili prva bimedijala, ili "veća", ili "strana kvadrata jednakog zbiru dve racionalne i medijalne površine".
Zaista, AB je ili veće od GD ili manje. Neka je, prvo, veće. Odmerimo racionalnu duž EZ, i konstruišimo na EZ pravougaonik EH jednak AB, sa širinom QK i na EZ pravougaonik QI jednak DG, sa širinom QK. Pošto je AB racionalno i jednako EH biće racionalno i EH. I pošto je konstruisano na racionalnoj duži EZ, a ima širinu EQ, biće racionalno i EQ i samerljivo po dužini sa EZ. Zatim pošto je GD medijalno i jednako QI, medijalna je i površina QI. A kako je konstruisana na racionalnoj duži EZ i ima širinu QK, biće racionalana i QK i nesamerljiva po dužini sa EZ. I pošto je GD medijalno, a AB - racionalno, biće AB nesamerljivo sa GD. Prema tome je i EH nesamerljivo sa QI. No EH je prema QI kao EQ prema QK, pa zbog toga je i EQ nesamerljivo po dužini sa QK. A obe te duži su racionalne. Na ovaj način su EQ i QK racionalne i samerljive samo u stepenu. Prema tome je EK binomijala podeljena tačkom Q. I pošto je AB veće od GD, a AB jednako EH, i GD jednako QI, biće EH veće od QI, a usled toga i EQ veće od QK. Sad je kvadrat ne EQ veći od kvadrata na QK za kvadrat na duži koja je ili samerljiva po dužini sa EQ ili nesamerljiva. Neka je, prvo, samerljiva. I veća QE je samerljiva sa odmerenom racionalnom duži EZ. Prema tome je EK prva binomijala. No ako je površina obuhvaćena dužima racionalnom i prvom binomijalom, onda je strana kvadrata jednakog toj površini binomijala. I prema tome strana kvadrata jednakog površini EI je binomijala. A tada je i strana kvadrata jednakog površini AD binomijala. No neka sad, kao drugo, kvadarat na EQ bude veći od kvadrata na QK za kvadrat na duži, koja je nesamerljiva sa EQ. I veća EQ je samerljiva po dužini sa odmerenom racionalanom duži EZ. A EK je tada četvrta binomijala. I EZ je racional. No ako je površina obuhvaćena dužima - racionalnom i četvrtom binomijalom, biće strana kvadrata jednakog toj površini iracionalna, takozvana "veća". Znači, strana kvadrata jednakog površini EI je "veća". Na taj način i strana kvadrata jednakog površini AD je "veća".

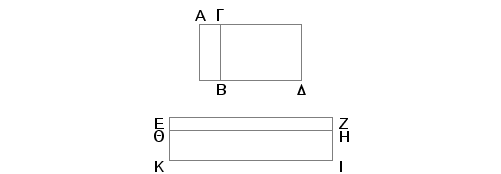
Neka je sad AB manje od GD. Biće tada i EH manje od QI. A zbog toga je i EQ manje od QK. No kvadrat na QK je veći od kvadrata na EQ za kvadrat ne duži koja je ili samerljiva sa QK ili nesamerljiva. Neka je, prvo, samerljiva po dužini. I manja EQ je samerljiva po dužini sa odmerenom racionalnom duži EZ. Znači EK je druga binomijala. A EZ je racionalna. No ako je površina obuhvaćena dužima - racionalnom i drugom binomijalom biće strana kvadrata jednakog toj površini prva bimedijala. Znači strana kvadrata jednakog površini EI je prva bimedijala. Na taj način i strana kvadrata jednakog površini AD je prva bimedijala. Neka sad kvadrat na QK bude veći od kvadrata na QE za kvadrat na duži koja nije samerljiva sa QK. I manja EQ je samerljiva sa odmerenom racionalnom duži EZ. Znači EK je peta binomijala. A EZ je racionalna. No ako je površina obuhvaćena dužima - racionalnom i petom binomijalom, biće strana kvadrata jednakog toj površini "strana kvadrata jednakog zbiru racionalne i medijalne površine". Na taj način strana kvadrata jednakog površini EI je "strana kvadrata jednakog zbiru racionalne i medijalne površine". A prema tome i strana kvadrata jednakog površini AD je "strana kvadrata jednaka zbiru racionalne i medijalne površine".
Na ovaj način, pri sabiranju racionalnog i medijalnog mogu se dobiti četiri iracionalnost: ili binomijala, ili prva bimedijala, ili "veća" ili "strana kvadrata jednakog zbiru racionalne i medijalne površine".