72.

Pri sabiranju dve među sobom nesamerljive medijalne površine mogu se dobiti dve ostale iracionalnost: ili druga bimedijala ili "strana kvadrata jednakog zbiru dve medijalne površine".

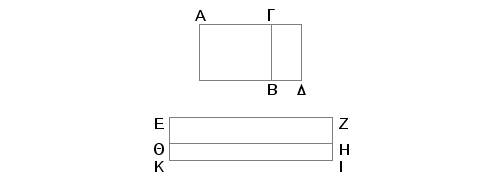
Neka se saberu dve među sobom nesamerljive medijalne površine AB i GD. Tvrdim da je strana kvadrata jednakog površini AD ili druga bimedijala ili "strana kvadrata jednakog zbiru dve medijalne površine".
Zaista, AB ili je veće od GD ili je manje. Neka, prvo, ako je to slučaj, AB bude veće od GD. Odmerimo racionalnu duž EZ, i neka površina EH, jednaka AB i konstruisana na EZ, ima širinu EQ, a površina QI, jednaka površini GD, ima širinu QK. I pošto je svaka od AB i GD medijalna, biće i svaka EH i QI medijalna. I konstruisane na racionalnoj duži ZE imaju širine EQ i QK. Na taj način svaka od EQ i QK je racionalna i nesamerljiva po dužini sa EZ. I pošto je AB nesamerljivo sa GD, a AB je jednako EH i GD jednako QI, biće nesamerljivo i EH sa QI. No EH je prema QI kao EQ prema QK. Prema tome je EQ nesamerljivo po dužini sa QK. Na ovaj način su EQ i QK racionalne, samerljive samo u stepenu. I prema tome je EK binomijala. Kvadrat na EQ je veći od kvadrata na QK za kvadrat na duži koja je ili samerljiva sa EQ ili nesamerljiva. Neka, prvo, ona bude samerljiva. I nijedna od EQ i QK nije samerljiva sa odmerenom racionalnom duži EZ. EK je tada treća binomijala. A EZ je racionalna. No ako je površina obuhvaćena dužima - racionalnom i trećom binomijalom, biće strana kvadrata jednakog toj površini druga bimedijala. Prema tome strana kvadrata jednakog površini EI, tj. AD biće druga bimedijala. Kvadrat na EQ je veći od kvadrata na QK za kvadrat na duži koja je nesamerljiva po dužini sa EQ. I nesamerljiva je svaka od EQ i QK sa EZ. Na ovaj način je EK šesta binomijala. No ako je površina obuhvaćena dužima - racionalnom i šestom binomijalom, biće strana kvadrata jednakog toj površini "strana kvadrata jednakog zbiru dve medijalne površine". Zbog toga je i strana kvadrata jednakog površini AD "strana kvadrata jednakog zbiru dve medijalne površine".
[Slično se dokazuje da je, ako je AB manje od GD, strana kvadrata jednakog površini AD ili druga medijala ili "strana kvadrata jednakog zbiru dve medijalne površine".]
Na ovaj način, pri sabiranju dve među sobom nesamerljive medijalne površine mogu se dobiti dve ospale iracionalnosti - ili druga bimedijala ili "strana kvadrata jednakog zbiru dve medijalne površine".

Binomijala i naredne iracionalne duži nisu iste ni sa medijalom ni među sobom. Zaista, kvadrat na medijali konstruisan na racionalnoj duži proizvodi širinu racionalnu i nesamerljivu po dužini sa onom duži na kojoj je konstruisan. A kvadrat na binomijali, konstruisan na racionalnoj duži, proizvodi kao širinu prvu binomijalu. Kvadrat na prvoj bimedijali konstruisan na racionalnoj duži, proizvodi kao širinu drugu binomijalu. Kvadrat na drugoj bimedijali, konstruisan na racionalnoj duži, proizvodi kao širinu treću binomijalu. Kvadrat na "većoj", konstruisan na racionalnoj duži, proizvodi kao širinu četvrtu binomijalu. Kvadrat na "strani kvadrata jednakog zbiru racionalne i medijalne površine", konstruisan na racionalnoj duži, proizvodi kao širinu petu binomijalu. Kvadrat na "strani kvadrata jednakog zbiru dve medijalne površine", konstruisan na racionalnoj duži, proizvodi kao širinu šestu binomijalu. Navedene širine se razlikuju kako od prve tako i među sobom; od prve zbog toga što je ona racionalna, a meću sobom zbog toga što nisu istog reda. Prema tome se i same iracionalnosti razlikuju među sobom.