77.
Ako se od duži oduzme duž, nesamerljiva u stepenu sa celom, a zbir kvadrata na njoj i na celoj je medijalan, i dvostruki pravougaonik obuhvaćen istim dužima racionalan, biće ostatak iracionalan. Neka se on zove "duž koja sa racionalnom obrazuje celo medijalno".*)
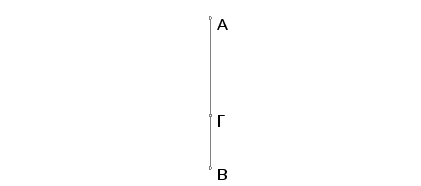
Neka se od duži AB oduzme duž BG, nesamerljiva u stepenu sa AB, i neka ispunjava navedene uslove. Tvrdim, da je ostatak gore navedena iracionalnost.
Zaista, pošto je zbir kvadrata na AB i na BG medijalan, a dvostruki pravougaonik kome su strane AB i BG racionalan, biće zbir kvadrata na AB i na BG nesamerljiv sa dvostrukim pravougaonikom kome su strane AB i BG. Znači i ostatak, kvadrat na AG, nesamerljiv je sa dvostrukim pravougaonikom kome su strane AB i BG. No dvostruki peavougaonik kome su strane AB i BG je racionalan, pa je kvadrat na AG iracionalan. Znači iracionalna je i AG. A ona se zove "duž koja saracionalnom obrazuje celo medijalno"
FOOTNOTETo je Euklidovo kratko izražavanje definicije tog pojma. Logički sadržajne izražavanje, analogno, recimo, definicija u stavu 40., bilo bi ovo: "strana kvadrata jednakog razlici medijalne i racionalne površine".}. A to je trebalo dokazati.