80.

Prvoj medijalnoj apotomi se se može dodati jedna jedina medijala, samo u stepenu samerljiva sa celom duži, i koja, zajedno sa celom duži, obuhvata racionalan pravougaonik.

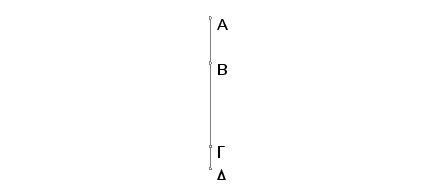
Neka je AB prva medijalna apotoma i BG njoj dodata duž. Znači, AG i GB su medijale, samerljive samo u stepenu, koje obuhvataju racionalan pravougaonik. Tvrdim da se duži AB ne može dodati nikakva druga medijala samerljiva samo u stepenu sa celom koja, zajedno sa celom, obuhvata racionalan pravougaonik.
Zaista, ako može neka se doda duž DB. Znači, AD i DB su medijale samerljive samo u stepenu, koje obuhvataju pravougaonik sa stranama AD i DB. I za koliko je zbir kvadrata na AD i na DB od dvostrukog pravougaonika sa stranama AD i DB, za toliko je veći i zbir kvadrata na AG i GB od dvostrukog pravougaonika sa stranama AG i GB, jer su oni ponovo veći za kvadrat na AB. Znači, posle permutovanja, zbir kvadrata na AD i na DB je za toliko veći od zbira kvadrata na AG i na GB, za koliko je dvostruki pravougaonik sa stranama AD i DB veći od dvostrukog pravougaonika sa stranama AG i GB. No dvostruki pravougaonik sa stranama AD i DB je veći od dvostrukog pravougaonika sa stranama AG i GB za racionalnu veličinu, jer su oba racionalni. A zbog toga je i zbir kvadrata na AD i na DB veći od zbira kvadrata na AG i na GB za racionalnu veličinu. A to je nemoguće, jer su oba medijalna, a medijalno od medijalnog ne može da bude veće za racionalnu veličinu.
Na ovaj način, prvoj medijalnoj apotom se može dodati jedna jedina medijala, samo u stepenu samerljiva sa celom duži, i koja, zajedno sa celom duži, obuhvata racionalan pravougaonik. A to je trebalo dokazati.