81.
Drugoj medijalnoj apotomi se može dodati jedna jedina medijala, samo u stepenu samerljiva sa celom duži, i koja, zajedno sa celom duži, obuhvata medijalan pravougaonik.
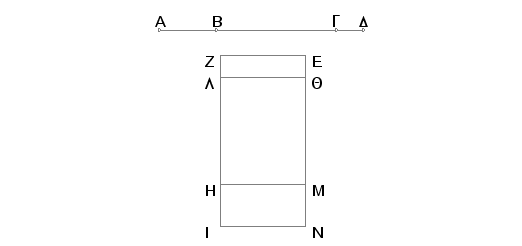
Neka je AB druga medijalna apotoma i BG njoj dodata duž. Znači, AG i GB su medijale samerljive samo u stepenu, koje obuhvataju medijalan pravougaonik. Tvrdim, da se ne može dodati duži AB nikakva druga medijala samerljiva samo u stepenu sa celom, koja zajedno sa celom obuhvata medijalan pravougaonik.
Zaista, ako može, neka se doda duž DB. Znači, AD i DB su medijale samerljive samo u stepenu, koje obuhvataju medijalan pravougaonik. Odmerimo racionalnu duž EZ i konstruišimo na EZ pravougaonik EH sa širinom EM jednak zbiru kvadrata na AG i na GB i oduzmimo površinu QH, sa širinom QM, jednaku dvostrukom pravougaoniku kome su strane AG i GB. Tada je ostatak EL jednak kvadratu na AB. Prema tome je AB strana kvadrata jednakog površini EL. Zatim konstruišimo na EZ površinu EI sa širinom EN jednaku zbiru kvadrata na AD i na DB. Takođe, je i površina EL jednaka kvadratu na AB. Znači ostatak QI jednak je dvostrukom pravougaoniku sa stranama AD i DB. I pošto su AG i GB medijale, pa prema tome je medijalan i zbir kvadrata na AG i na GB. A on je jednak površini EH, znači i površina EH je medijalna. A ona je konstruisana na racionalnoj duži EZ sa širinom EM. Zbog toga je EM racionalna duž nesamerljiva po dužini sa EZ. Zatim, pošto je pravougaonik kome su strane AG i GB medijalan, biće medijalan i dvostruki pravougaonik kome su strane AG i GB. I on je jednak površini QH. Znači i QH je medijalna. A ova je konstruisana na racionalnoj duži EZ sa širinom QM. Prema tome je racionalna i duž QH i nesamerljiva po dužini sa EZ. I pošto su AG i GB samerljive samo u stepenu, onda je AG nesamerljiva po dužini sa GB. No kako AG stoji prema GB tako i kvadrat na AG stoji prema pravougaoniku kome su strane AG i GB. Znači kvadrat na AG je nesamerljiv sa pravougaonikom kome su strane AG i GB. No sa kvadratom na AG samerljiv je zbir kvadrata na AG i na GB, a sa pravougaonikom kome su strane AG i GB je samerljiv dvostruki pravougaonik sa istim stranama. Prema tome je zbir kvadrata na AG i na GB nesamerljiv sa dvostrukim pravougaonikom kome su strane AG i GB. No zbir kvadrata na AG i na GB jednak je površini EH, a dvostruki pravougaonik sa stranama AG i GB jednak je HQ. Dakle, EH je nesamerljivo sa QH. Ali EH je prema QH kao što je EM prema QM. Znači EM je nesamerljivo po dužini sa MQ. I obe te duži su racionalne. Prema tome su EM i MQ racionalne, samerljive samo u stepenu. Na taj način, EQ je apotoma a QM je njoj dodata duž. Na sličan način se dokazuje da joj se može dodati i QN. Prema tome se apotomi mogu dodati i jedna i druga duž, koje su samerljive sa celom samo u stepenu. A to je nemoguće.
Na taj način, drugoj medijalnoj apotomi se može dodati jedna jedina medijala, samo u stepen samerljiva sa celom duži, i koja, zajedno sa celom duži, obuhvata medijalan pravougaonik. A to je trebalo dokazati.