85.
Naći prvu apotomu.
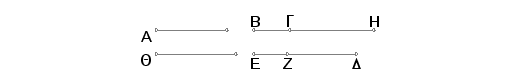
Neka je A data racionalna duž i BH duž samerljiva po dužini sa A. Stoga je i BH racionalna. Uzmimo dva kvadratna broja DE i EZ, čija razliak ZD nije kvadratni broj. Onda ED ne stoji u donosu prema DZ kao kvadratni broj prema kvadratnom broju. Načinimo tako da ED prema DZ bude kao kvadrat na BH prema kvadratu na HG. Biće tada kvadrat na BH samerljiv sa kvadratom na HG. Ali kvadrat na BH je racionalan, pa će i kvadrat na HG biti racionalan, prema tome je racionalna i duž HG. I pošto ED ne stoji u odnosu prema DZ kao kvadratni broj prema kvadratnom, neći ni kvadrat na BH stojati u odnosu prema kvadratu na HG kao kvadratni broj prema kvadratnom broju. Prema tome je duž BH nesamerljiva sa duži HG po dužino. A obe su racionalne. Na ovaj način BH i HG su racionalne i samerljive samo u stpenu. Dakle BG je apotoma.
Tvrdim da je baš prva.
Zaista, neka ono čime se razlikuje kvadrat na BH od kvadrata na BG bude kvadrat na Q. I pošto je ED prema ZD kao kvadrat na BH prema kvadratu na HG, biće, posle zamene jednog člana drugim, DE prema EZ kao kvadrat na HB prema kvadratu na Q. Ali DE je u odnosu prema EZ kao kvadratni broj prema kvadratnom broju, jer je svaki kvadrat. Prema tome kvadrat na HB je u odnosu prema kvadratu Q kao kvadratni broj prema kvadratnom broju. Na ovaj način BH je samerljivo po dužini sa Q. I kvadrat na BH je veći od kvadrata na HG za kvadrat na Q. Dakle kvadrat na BH je veći od kvadrata na HG za kvadrat na duži samerljivoj po dužini sa BH. I pri tome je cela duž BH samerljiva po dužini sa datom racionalnom duži A. Dakle je BG prva apotoma.
Na ovaj način je nađena prva apotoma. A to je trebalo dokazati.