89.
Naći petu apotomu.
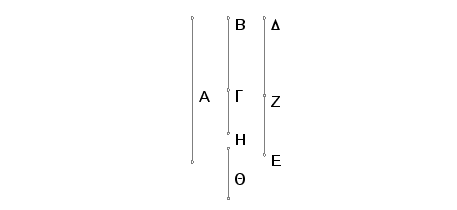
Uzmimo racionalnu duž A i duž GH samerljivu po dužini sa A. Tada je i duž GH racionalna. Uzmimo dva broja DZ i ZE i to tako da se DE ponovo ne odnosi prema svakom od brojeva DZ i ZE kao kvadratni broj prema kvadratnom broju. I načinimo tako da ZE prema ED bude kao kvadrat na GH prema kvadratu na HB. Znači da je racionalan i kvadrat na HB, te prema tome je racionalna i duž BH. I pošto je DE prema EZ kao kvadrat na BH prema kvadratu HG, a DE prema EZ nije u odnosu kvadratnog broja prema kvadratnom broju, na kvadrat na BH neće biti prema kvadratu na HG u odnosu kvadratnog broja prema kvadratnom broju. Znači duž BH je nesamerljiva po dužini sa HG. A obe su racionalne. Prema tome su BH i HG racionalne samerljive samo u stepenu. Na ovaj način BG je apotoma.
Tvrdim da je baš peta.
Zaista, neka ono čime je kvadrat na BH veći od kvadrata na HG bude kvadrat na Q. Pošto je sad kvadrat na BH prema kvadratu na HG kao DE prema EZ, biće posle zamene jednog člana drugim, ED prema AZ kvadrat na BH prema kvadratu na Q. No ED ne stoji u odnosu prema DZ kao kvadratni broj prema kvadratnom broju, pa ni kvadrat na BH ne stoji u odnosu prema kvadratu na Q kao kvadratni broj prema kvadratnom broju. Znači duž BH je nesamerljiva po dužini sa Q. A kvadrat na BH je veći od kvadrata na HG za kvadrat na Q. Prema tome kvadra na HB je veći od kvadrata na HG za kvadrat na duži koja je nesamerljiva sa HB. I dodatak GH je samerljiv po dužini sa datom racionalnom duži A. Dakle BG je peta apotoma.
Na ovaj način je nađena peta apotoma BG. A to je trebalo dokazati.