93.

Ako je površina obuhvaćena racionalnom duži i trećom apotomom, onda kvadrat, jednak toj površini, ima za stranu drugu apotomu medijale.

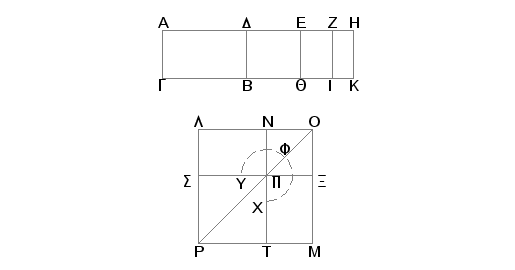
Neka je površina AB obuhvaćena racionalnom duži AG i trećom apotomom AD. Tvrdim da je strana kvadrata, jednakog površini AB, druga apotoma medijale.
Zaista, neka je DH dodatak za AD. Prema tome su duži AH i HD racionalne i samerljive samo u stepenu, i nijedna od AH i HD nije samerljiva po dužini sa datom racionalnom duži AG, i kvadrat na celoj duži AH je veći od kvadrata na duži DH za kvadrat na duži samerljivoj sa AH. Pošto je sad kvadrat na AH veći od kvadrata na HD za kvadrat na duži samerljivoj sa AH, onda, ako se konstruiše na AH paralelogram jednak četvrtini kvadrata na HD sa vkadratnom dopunom, on će podeliti AH na samerljive delove. Prepolovimo sad DH tačkom E i konstruišimo na AH paralelogram jednak kvadratu na EH sa kvadratnom dopunom, i neka to bude paralelogram obuhvaćen sa AZ i ZH. I povucimo kroz tačke E, Z, H prave EQ, ZI, HK paralelne pravoj AG. Stoga će duži AZ i ZH biti samerljive. A tada su samerljive i površine AI i ZK. I pošto su AZ i ZH samerljive po dužini, biće i AH samerljivo po dužini sa svakom od AZ i ZH. No AH je racionalna duž i nesamerljiva po dužini sa AG, te znači da su takve i AZ i ZH. Prema tome je svaka od površina AI i ZK medijalna. Zatim, pošto je DE samerljivo po dužini sa EH, biće i DH samerljivo po dužini sa svakim od DE i EH. No duž HD je racionalna i nesamerljiva po dužini sa AG. Prema tome je racionalna i svaka od DE i EH i nesamerljiva po dužini sa AG. A svaka od površina DQ i EK je medijalna. I pošto su AH i HD samerljive samo u stepenu, biće AH nesamerljivo po dužini sa HD. No AH je samerljivo po dužini sa AZ, a DH sa EH, zbog toga je AZ nesamerljivo po dužini sa EH. Kako je AZ prema EH kao AI prema EK, biće nesamerljivo i AI sa EK.
Konstruišimo sad kvadrat LM jednak površini AI i oduzmemo od njega kvadrat NX, jednak površini ZK, sa istim uglom pri LM. Prema tome su kvadrati LM i NX na istoj dijagonali. Neka njihova dijagonala bude OP i dopunimo sliku. Pošto je sad površina obuhvaćena od AZ i ZH jednaka kvadratu na EH, biće AZ prema EH kao EH prema ZH. No AZ je prema EH kao AI prema EK, a EH je prema ZH kao EK prema ZK, i prema tome je AI prema EK i EK prema ZK. Na ovaj način je EK srednja proporcionala za AI i ZK. A za kvadrate LM i NX srednja proporcionala je površina MN. I površina AI jednaka je kvadratu LM, a površina ZK kvadratu NX pa prema tome je površina EK jednaka površini MN. No MN je jednako LX, a EK jednako DQ. Zbog toga je cela površina DK jednaka gnomonu UFX sa kvadratom NX. Isto tako i cela površina AK je jednaka zbiru kvadrata LM i NX. A tada je ostatak AB jednak površini ST. tj. kvadratu na LN. Na ovaj način je LN strana kvadrata jednakog površini AB.
Tvrdim da je LN druga apotoma medijale.
Zaista, pošto je dokazano da su površine AI i ZK medijalne i jednake kvadratima na LO i ON, biće medijalni i svaki od kvadrata na LO i na ON, pa prema tome je medijala i svaka od LO i ON. I pošto je AI samerljivo sa ZK, biće i kvadrat na LO samerljiva sa kvadratom na ON. Zatim, pošto je dokazano da je AI nesamerljivo sa EK, biće nesamerljivo i LM sa MN, tj. kvadrat na LO sa pravougaonikom obuhvaćenim sa LO i ON. Zbog toga je i duž LO nesamerljiva po dužini sa ON. Na taj način su LO i ON medijalne samerljive samo u stepenu.
Tvrdim da one i obuhvataju medijalnu površinu.
Zaista, pošto je dokazano da EK medijalna površina i ona je jednaka površini obuhvaćenoj sa LO i ON, biće i ta površina, obuhvaćena sa, LO i ON medijalna. Znači LO i ON su medijale samerljive samo u stepenu koje obuhvataju medijalnu površinu. Prema tome je LN druga apotoma medijale. I ona je strana kvadrata jednakog površini AB.
Na ovaj način je strana kvadrata, jednakog površini AB, druga apotoma medijale. A to je trebalo dokazati.