95.
Ako je površina obuhvaćena racionalnom duži i petom apotomom. onda kvadrat, jednak toj površini, ima za stranu duž koja se racionalnom obrazuje celo medijalno.
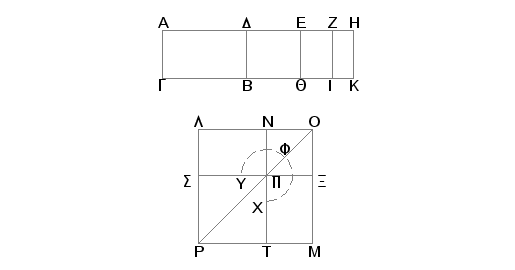
Neka je površina AB obuhvaćena racionalnom duži AG i petom apotomom AD. Tvrdim da je strana kvadrata, jednakog površini AB duž koja sa racionalnom obrazuje celo medijalno.
Zaista, neka je DH dodatak za AD. Prema tome su duži AH i HD racionalne samerljive samo u stepenu i dodatak HD je samerljiv po dužini sa datom racionalnom duži AG, a kvadrat na celoj duži AH je veći od kvadrata na DH za kvadrat na duži nesamerljivoj sa AH. Onda, ako se konstruiše na H paralelogram jednak četvrtini kvadrata na HD sa kvadratnom dopunom, on će podeliti AH na nesamerljive delove. Prepolovimo DH tačkom E i konstruišimo na AH paralelogram jednak kvadratu na EH sa kvadratnom dopunom i neka to bude paralelogram obuhvaćen sa AZ i ZH. Stoga će AZ biti nesamerljivo po dužini sa ZH. I pošto je AH nesamerljivo po dužini sa GA, a oba su racionalni, biće AK medijalno. Zatim, pošto je DH racionalno i samerljivo po dužini sa AG, biće i DK racionalno. Konstruišimo sad kvadrat LM jednak AI i oduzmimo od njega kvadrat NX jednak ZK sa istim uglom LOM. Tada su kvadrati LM i NX na istoj dijagonali. Neka OP bude njihova dijagonala i dopunimo sliku. Na sličan način se dokazuje da je LN strana kvadrata jednakog površini AB.
Tvrdim da je LN "duž koja sa racionalnom obrazuje celo medijalno".
Zaista, pošto je dokazano da je AK medijalno i jednako zbiru kvadrata na LO i na ON, onda je taj zbir kvadrata na LO i na ON medijalan. Zatim, pošto je DK racionalno i jednako dvostrukom pravougaoniku obuhvaćenom sa LO i ON, biće i taj pravougaonik racionalan. A kako je AI nesamerljivo sa ZK, biće i kvadrat na LO nesamerljiv sa kvadratom na ON. Prema tome su LO i ON, nesamerljivi u stepenu, zbir kvadrata na njima je medijalan i dvostruki pravougaonik od njih racionalan. Na ovaj način, ostatak, duž LN je iracionalna i zove se "duž koja sa racionalnom obrazuje celo medijalno", a jednaka je strani kvadrata jednakog površini AB.
Na ovaj način je strana kvadrata, jednakog površini AB, "duž koja sa racionalnom obrazuje celo medijalno". A to je trebalo dokazati.