98.

Pravougaonik, konstruisan na racionalnoj duži i jednak kvadratu na prvoj medijalnoj apotomi, ima za širinu drugu apotomu.

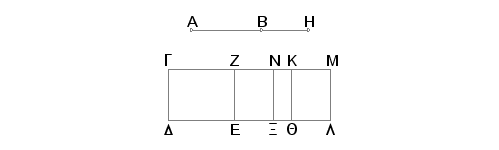
Neka je AB prva medijalna apotoma, GD racionalna duž i na GD je konstruisan pravougaonik GE, jednak kvadratu na AB, kome j širina GZ. Tvrdim da je GZ druga apotoma.
Zaista, neka je BH dodatak za AB. Tada su AH i HB medijale, samerljive u stepenu, koje obuhvataju racionalnu površinu. I konstruišimo na GD pravougaonik GQ, jednak kvadratu na AH, sa širinom KM. Prema tome je cela površina GL jednaka zbiru kvadrata na AH i na HB. Znači i GL je medijalna površina. I konstruisana je na racionalnoj duži GD i ima za širinu GM. Na ovaj način GM je racionalna duž i nesamerljiva po dužini sa GD. I pošto je površina GL jednaka zbiru kvadrata na AH i na HB, a kvadrat na AB jednak je površini GE, biće ostatak, dvostruki pravougaonik sa stranama AH i HB, jednak površini ZL. No dvostruki pravougaonik sa stranama AH i HB je racionalan. Prema tome je racionalna i površina ZL. I konstruisana je na racionalnoj duži ZE i ima za širinu ZM. Na taj način je racionalna i duž ZM i samerljiva po dužini sa GD. Pošto je sad zbir kvadrata na AH i na HB, tj. površina GL, medijalna, a dvostruki pravougaonik sa stranama AH i HB, tj. površina ZL, racionalan, biće površina GL nesamerljiva sa površinom ZL. No GL je prema ZL kao GM prema ZM, pa prema tome i duž GM je nesamerljiva po dužini sa ZM. A obe su racionalne. Znači duži GM i MZ su racionalne i samerljive samo u stepenu. Dakle GZ je apotoma.
Tvrdim da je druga.
Zaista, prepolovimo ZM tačkom N i povucimo kroz N pravu NX paralelnu pravoj GD. Tada je svaka od površina od ZX i NL jednaka pravougaoniku sa stranama AH i HB. I pošto je za kvadrate na AH i na HB srednja praporcionalna pravougaonik sa stranama AH i HB, i kvadrat na AH jednak je GQ, pravougaonik sa stranama AH i HB jednak NL i kvadrat na BH jednak je KL, onda je srednja praporcionala za GQ i KL povrešina NL. I prema tome je GQ prema NL kao NL prema KL. No GQ je prema NL kao GK prema NM, a NL je prema KL kao NM prema MK. Prema tome je GK prema NM kao NM prema KM, to znači da je pravougaonik obuhvaćen sa GK i KM jednak kvadratu na NM, tj. četvrtini kvadrata na ZM [i pošto je kvadrat na AH samerljiv sa kvadratom na BH, samerljiva je i površina GQ sa površinom KL, tj. duž GK sa duži KM]. Sad, pošto su GM i MZ dve nejednake duži i na većoj GM je konstruisan pravougaonik jednak četvrtini kvadrata na MZ, sa kvadratnom dopunom, naime pravougaonik obuhvaćen stranama GK i KM, a i GK je samerljivo sa KM, biće kvadrat na GM veći od kvadrata na MZ za kvadrat na duži samerljivoj sa GM. I dodatak ZM je samerljiv po dužini sa datom racionalnom duži GD. Prema tome je GZ druga apotoma.
Na ovaj način, pravougaonik, konstruisan na racionalnoj duži i jednak kvadratu na prvoj medijalnoj apotomi, ima za širinu drugu apotomu. A to je trebalo dokazati.