17.
Ako se dve prave preseku paralelnim ravnima, njihovi otsečci su u istoj razmeri.
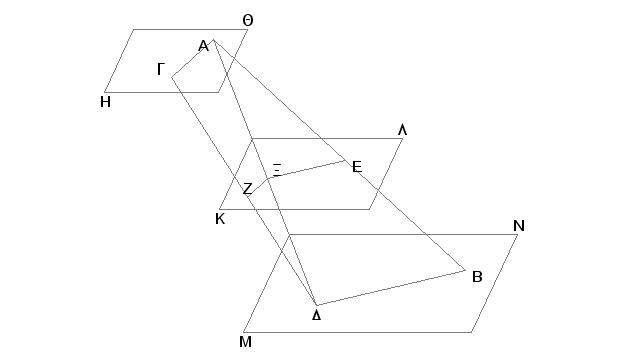
Zaista, neka su dve prave AB i GD presečene paralelnim ravnima HQ, KL, MN u tačkama A, E, B, G, Z, D. Tvrdim da je duž AE prema duži EB kao GZ prema ZD.
Zasta. spojimo AG, BD, AD i neka AD prodire ravan KL u tački X, pa spojimo EX i XZ. Pošto su dve paralelne ravni, KL i MN, presečene sa ravni EBDX, biće njihovi zajednički preseci EX i BD paralelni [XI.16]. Iz istih razloga, pošto su dve paralelne ravni, HQ i KL, presečene sa ravni AXZG, biće i njihovi preseci, AG i XZ, paralelni [XI.16]. I pošto je u trouglu ABD povučena prava EX paralelno strani BD, biće AE prema EB kao EX prema XD [VI.2]. Dalje, pošto je u trouglu ADG prava XZ povučena paralelno strani AG, biće AX prema XD kao GZ prema ZD [VI.2]. A dokazano je da je AX prema XD kao i AE prema EB. Prema tome je AE prema EB kao GZ prema ZD [V.11].
Na ovaj način, ako se dve prave preseku paralelnim ravnima, njihovi otsečci su u istoj razmeri. A to je trebalo dokazati.