1.
Slični mnogouglovi, upisani u krugove, odnose se jedan prema drugom kao kvadrati na prečnicima.
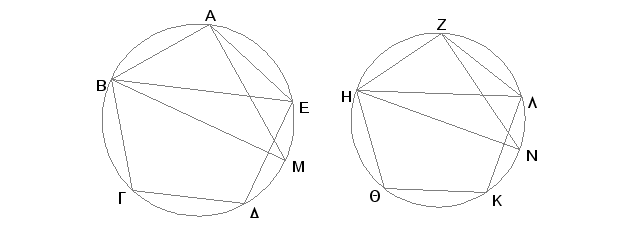
Neka su ABG, ZHQ krugovi, i ABGDE, ZHQKL upisani slični mnogouglovi, i neka su BMZHN prečnici krugova. Tvrdim da je kvadrat na BM prema kvadratu na HN kao mnogougao ABGDE prema ZHQKL.
Zaista povucimo BE, AM, HA, ZN. Pošto je mnogougao ABGDE sličan mnogouglu ZHQKL, ugao BAE je jednak uglu HZL i duž BA je prema duži AE kao HZ prema ZL [VI, Def. 1]. Sad imamo dva trougla, BAE i HZL, i ugao BAE jednog jednak je uglu HZL drugog, a kraci tih uglova su proporcionalni. Tada trouglovi ABE i ZHL imaju jednake uglove [VI.6]. Prema tome je ugao AEB jednak uglu ZLH. Ali ugao AEB je jednak uglu AMB, pošto su nad istim lukom [III.27]. I ugao ZLH je jednak uglu ZNH; pa i ugao AMB je jednak uglu ZNH. A i prav ugao BAM je jednak pravom uglu HZN [III.31]. Stoga je i preostali ugao jednak preostalom uglu [I.32]. Prema tome trouglovi ABM i ZHN imaju jednake uglove. Dakle, razmera BM prema HN jednaka je razmeri BA prema HZ [VI.4]. Ali razmera dvaput viša od razmere BM prema HN je jednaka razmeri kvadrata na BM prema kvadratu na HN. A razmera dvaput viša od razmere BA prema HZ je jednaka razmeri mnogougla ABGDE prema mnogouglu ZHQKL [VI.20]. Prema tome je kvadrat na BM prema kvadratu na HZ kao mnogougao ABGDE prema mnogouglu ZHQKL.
Na ovaj način, slični mnogouglovi, upisani u krugove, odnose se jedan prema drugom kao kvadrati na prečnicima. A to je trebalo dokazati.