17.

Ako su date dve sfere sa istim centrom, upisati u veću sferu poliedarsko telo koje ne dodiruje površinu manje sfere.

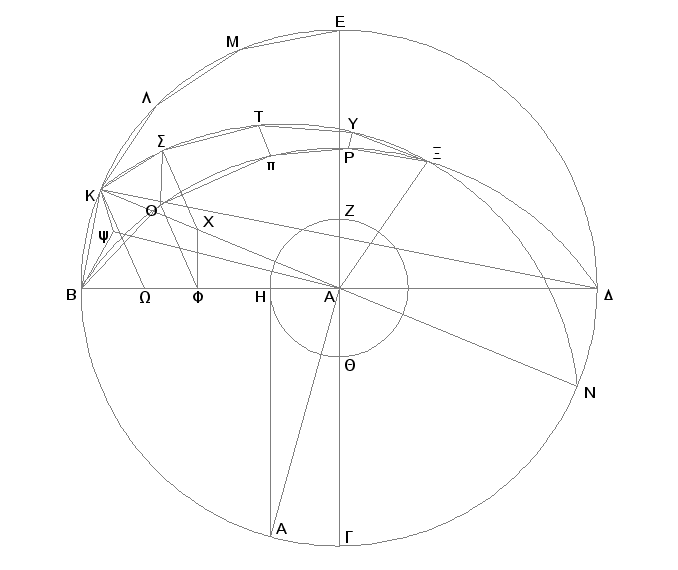
Neka su date dve sfere sa istim centrom A. Treba u veću sferu upisati poliedarsko telo koje ne dodiruje površinu manje sfere.
Presecimo ove sfere nekom ravni kroz centar. Tada su preseci krugovi, jer se sfera dobija obrtanjem polukruga oko nepomičnog prečnika [XI, Def. 14], te tako ma u kom položaju mi zamislili taj plukrug, ravan kroz isti daje krug na površini sfere. I jasno je da je taj krug najveći mogući, jer je prečnik sfere, koji je u isto vreme prečnik i polusfere, a prirodno, i kruga, najveća duž koja može da stane u krug ili u sferu. Neka sad BGDE bude krug veće sfere, a ZHQ krug manje sfere; povucimo dva prečnika BD i GE, upravna jedan na drugi. To su dva kruga sa istim centrom, BGDE i ZHQ pa upišimo u veći krug BGDE jednakostrani mnogougao sa parnim brojem strana, koji ne dodiruje manji krug ZHQ. Neka su BK, KL, LM, ME njegove strane u kvadratu BE; pa povucimo pravu KA, produžimo do N, zatim iz tačke A povucimo normalu AX na ravan kruga BGDE i neka ova seče površinu sfere u tački X, pa kroz AX i svaku od BD i KN konstruišimo ravni. One će na površini sfere obrazovati velike krugove. Uzmimo da obrazuju one krugove kojima pripadaju krugovi BXD i KXN na prečnicima BD i KN. Pošto je XA upravna na ravni kruga BGDE i svaka ravan kroz XA je upravna na ravni kruga BGDE [XI.18], biće i polukrugovi BXD i KXN upravni na ravni kruga BGDE. A tako su BED, BXD i KXN jednaki polukrugovi, jer su na jednakim prečnicima BD i KN, biće jednaki među sobom i kvadranti BE, BX i KX. I prema tome koliko je strana mnogougla u kvadrantu BE toliko će biti duži jednakih BK, KL, LM, ME u jednakim kvadrantima BX i KX. Upišimo i nacrtajmo BO, Op, pP, PX, KS, ST, TU, UX, zatim spojimo SO, Tp, UP, pa iz tačke O i S spustimo normale na ravan kruga BGDE [XI.11]. One će pasti na BD i na KN, što su preseci ravni, jer su ravni BXD i KXN upravne na ravni kruga BGDE [XI, Def. 4]. Neka to budu normale OF i SX pa povucimo XF. I pošto su na jednakim polukrugovima, BXD i KXN, odmereni jednaki lukovi BO i XS, i povučene normale OF i SX biće OF jednako SX i BF jednako KX [III.27, I.26]. A pošto je celo BA jednako celom KA, biće i ostatak FA jednak ostatku XA. Prema tome je BF prema FA kao KX prema XA i XF je paralelno sa KB [VI.2]. A pošto je svako od OF i SX upravno na ravni kruga BGDE, biće OF paralelno SX [XI.6]. A dokazano je da je jedno drugom jednako. Prema tome su XF i SO među sobom jednaki i paralelni [I.33]. I pošto je XF paralelno SO a XF je paralelno KB, onda je i SO paralelno KB [XI.9]. Sad povuccimo BO i KS. Tada je KBOS ravan četvorougao, jer, ako postoje dve paralelne prave i na svakoj od njih su uzete dve proizvoljne tačke, dve prave, koje spajaju te tačke, biće u ravni paralelnih pravih [XI.7]. Iz istih razloga je i svaki od četvorouglova SOpT i TpPU u ravni. A i trougao UPX je u ravni. Ako zamislimo prave što spajaju tačku A sa tačkama O, S, p, T, p, U, onda se obrazuje neka poliedarska figura koja se nalazi između lukova BX i KX i koja je obrazovana od piramida koje imaju u osnovama četvorouglove KBOS, SOpT, TpPU i trougao UPX, a vrh u tački A. Ako na svakoj od strana KL, LM, ME izvršimo iste konstrukcije kao i na BK, i isto tako i u ostalim trima kvadrantima, dobiva se figura poliedra upisanog u sferu i sastavljenog od piramida sa četvorouglovima i trouglom UPX u osnovama, a takođe i od osnova u sličnom položaju sa njima, i sa vrhom u tački A.
Tvrdim da navedeni poliedar neće dodirivati površinu manje sfere na čijoj je površini krug ZHQ.
Iz tačke A spustimo normalu AY na ravan četvorougla KBOS i neka ona prodire tu ravan u tački Y [XI.11], pa povucimo YB i YK. Pošto je AY normala na ravni četvorougla KBOS, ona će biti upravna i na svakoj pravoj u toj ravni koja je seče [XI, Def. 3]. Prema tome je AY upravna i na svakoj od pravih BY i YK. I pošto je AB jednako AK biće i kvadrat na AB jednak kvadratu na AK. No kvadrat na AB jednak je zbiru kvadrata na AY i na YB [I.47], jer je ugao kod Y prav. I kvadrat na AK jednak je zbiru kvadrata AY i YK [I.47]. Znači zbir kvadrata na AY i YB jednak je zbiru kvadrata na AY i na YK. Oduzmimo zajednički kvadrat na AY. Tada je i preostali kvadrat na BY jednak preostalom kvadratu na YK. Znači i BY jednako je YK. Na sličan način se dokazuje da su i prave povučene iz Y u O i u S jednake svakoj od pravih BY i YK. Prema tome krug kome je centar u Y i duži YB i YK kao poluprečnici proćiće i kroz tačke O i S, a četvorougao KBOS biće u krugu.
I pošto je KB veće od XF, a XF je jednako SO , veće je i KB od SO. No KB je jednako i KS i BO. Prema tome je i svako od KS i BO veće od SO. I pošto je četvorougao KBOS u krugu, duži KB, BO, KS su jednake, a OS je manje i BY je poluprečnik, biće kvadrat na KB veći od udvostručemog kvadrata na BY. Povucimo iz K normalu KW na BF. Sad pošto je BD manje od dvostrukog DW, i BD je prema DW kao pravougaonik od DB i BW prema pravougaoniku od DW i WB, onda će, kad se na BW konstruiše kvadrat i dopuni paralelogram na WD, pravougaonik od DB i BW biti manji od dvostrukog pravougaonika od DW i WB. I ako se povuče KD biće pravougaonik od DB i BW jednak kvadratu na BK i pravougaonik od DW i WB jednak kvadratu na KW. I prema tome je kvadrat na KB manji od udvostručenog kvadrata na BW. Ali kvadrat na KB je veći od udvostručenog kvadrata na BY pa je prema tome i kvadrat na KW veći od kvadrata na BY. No kako je BA jednako KA, biće i kvadrat na BA jednak kvadratu na AK. I zbir kvadrata na BY i na YA jednak je kvadratu na BA, a zbir kvadrata na KW i na WA kvadratu na KA [I.47], pa je prema tome zbir kvadrata na BY i na YA jednak zbiru kvadrata na KW i na WA, ali kvadrat na KW je veći od kvadrata na BY. Znači, preostali kvadrat na WA manji je od kvadrata na YA. Zbog toga je AY veće od AW. Tim pre je AY veće od AH. I AY je normala spuštena na jednu od osnova poliedara, a AH je normala povučena prema površini manje sfere. Prema tome poliedar ne dodiruje površinu manje sfere.
Na ovaj način, za dve sfere sa istim centrom u veću sferu je upisano poliedarsko telo koje ne dodiruje površinu manje sfere. A to je trebalo izvesti.