Svaka piramida sa trouglom osnovom može se podeliti na dve jednake piramide sa trouglim osnovama, slične jedna drugoj i celoj piramidi, i na dve jednake prizme; zbir te dve prizme je veći od od polovine cele piramide.

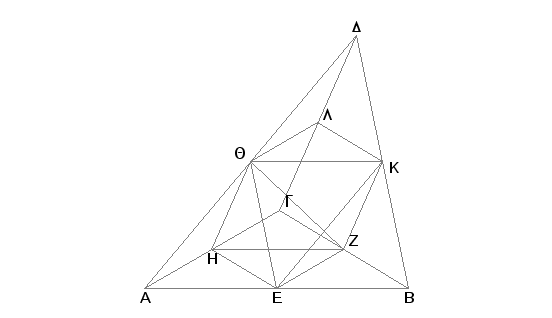
Neka bude data piramida sa trouglom osnovom ABG i vrhom u tački D. Tvrdim da se piramida ABGD može podeliti na dve jednake piramide sa trouglim osnovama, slične jedna drugoj i celoj piramidi, i na dve jednake prizme, i da je zbir te dve prizme veći od polovine cele piramide.
Zaista, prepolovimo AB, BG, GA, AD, DB, DG tačkama E, Z, H, Q, K, L i spojimo QE, EH, HQ, QK, KL, LQ, KZ, ZH. Pošto je AE jednako EB i AQ jednako DQ, prava EQ je paralelna pravoj DB [VI.2]. Iz istih razloga biće i prava QK paralelna pravoj AB. Prema tome QEBK je paralelogram. Stoga je QK jednako EB [I.34]. No EB je jednako EA, pa je stoga i AE jednako QK. I AQ je jednako QD. Dve duži AE i AQ jednake su dvema dužima KQ i QD, svaka svakoj; i ugao EAQ jednak je uglu KQD, pa je, znači, i osnovica EQ jednaka osnovici KD [I.4]. Prema tome je trougao AEQ jednak i sličan trouglu QKD. Iz istih razloga i trougao AQH jednak je i sličan trouglu QLD. I pošto su dve prave EQ i QH, koje se seku, paralelne sa dvema pravima KD i DL, koje se seku, a prve prave nisu u istoj ravni sa drugim, one obrazuju jednake uglove [XI.10]. Prema tome je ugao EQH jednak uglu KDL. I pošto su dve duži EQ i QH jednake dvema dužima KD i DL, svaka svakoj, i ugao EQH jednak uglu KDL, biće i osnovica EH jednaka osnovici KL [I.4]. Na ovaj način trougao EQH jednak je i slična trouglu KDL. Iz istih razloga je i trougao AEH jednak i sličan trouglu QKL. Na ovaj način je piramida kojoj je osnova trougao AEH i vrh u tački Q jednaka i slična piramidi kojoj je osnova trougao QKL i vrh u tački D [XI, Def. 10]. I pošto je u trouglu ADB povučena prava QK paralelno jednoj od strana, strani AB, trougao ADB imaće jednake uglove kao i trougao DQK [I.29], a strane su im proporcionalne. Prema tome je trougao ADB sličan trouglu DQK [VI, Def. 1]. Iz istih razloga i trougao DBG biće sličan trouglu DKL, a trougao ADG trouglu DLQ. I pošto su dve prave BA i AG, koje se seku, paralelne sa dvema pravima KQ i QL, koje se takođe seku, ali sa prvima nisu u istoj ravni, one obrazuju jednake uglove [XI.10]. Dakle ugao BAG jednak je uglu KQL. I pošto je BA prema AG kao KQ prema QL, biće trougao ABG sličan trouglu QKL. I na taj način je piramida kojoj je osnova trougao ABG i vrh u tački D slična piramidi kojoj je osnova trougao QKL i vrh u tački D. Dokazano je međutim da je piramida kojoj je osnova trougao QKL i vrh u tački D slična piramidi kojoj je osnova trougao AEH i vrh u tački Q jer je i piramida kojoj je osnova trougao ABG i vrh u tački D slična piramidi kojoj je osnova trougao AEH i vrh u tački Q. Prema tome je svaka od piramida AEHQ i QKLD slična celoj piramidi ABGD.
I pošto je BZ jednako ZG, paralelogram EBZH je dvaput veći od trougla HZG. A kako su dve prizme, ako imaju jednake visine i jedna za osnovu paralelogram, a druga trougao, uz to paralelogram dvaput veći od trougla, jednake [XI.39], biće i prizma obuhvaćena dvama trouglima, BKZ i EQH, i trima paralelogramima, EBZH, EBKQ, QKZH, jednaka prizmi obuhvaćenoj dvama trouglima HZG i QKL i trima paralelogramima KZGL, LGHQ i QKZH. I jasno je da će svaka prizma, naime, prva, kojoj je osnova paralelogram EBZH i naspramna ivica QK, i druga kojoj je osnova trougao HZG i naspramni trougao QKL biti veća od svake piramide sa osnovama AEH i QKL i vrhovima Q i D, pošto, ako povučemo prave E Z i EK, biće prizma čija je osnova paralelogram EBZH i naspramna ivica QK veća od piramide kojoj je osnova trougao EBZ i vrh tačka K. Međutim je piramida kojoj je osnova trougao EBZ i vrh tačka K jednaka piramidi kojoj je osnova trougao AEH i vrh tačka Q, pošto su one obuhvaćene jednakim i sličnim ravnima (mnogouglovima). Na taj način je i prizma kojoj je osnova paralelogram EBZH i naspramna ivica QK veća od piramide kojoj je osnova trougao AEH i vrh u tački Q. No prizma kojoj je osnova paralelogram EBZH i naspramna ivica QK jednaka je prizmi kojoj je osnova trougao HZG i naspramni trougao QKL. A piramida kojoj je osnova trougao AEH i vrh u tački Q jednaka je piramidi kojoj je osnova trougao QKL i vrh u tački D. Znači dve navedene prizme veće su od dve navedene piramide, čije su osnove trouglovi AEH i QKL i vrhovi u tačkama Q i D.
Na ovaj način cela piramida kojoj je trougao ABG u osnovi i vrh u tački D može se podeliti na dve među sobom jednake (slične celoj) piramide i na dve jednake prizme, čiji je zbir veći od polovine cele piramide. A to je trebalo dokazati.