13.
Ako je valjak presečen nekom ravni paralelnom sa naspramnim ravnima, otseći će se osa prema osi kao valjak prema valjku.
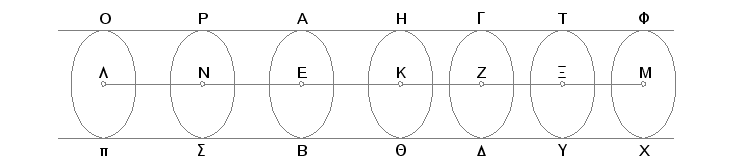
Neka je valjak AD presečen sa ravni HQ, koja je paralelna sa naspramnim ravnima AB i GD, i neka ravan HQ seče osu u tački K. Tvrdim da je valjak BH prema valjku HD kao osa EK prema osi KZ
Zaista, produžimo osu EZ na obe strane do tačaka L i M, odmerimo nekoliko duži EN, NL jednakih EK, i nekoliko duži ZX, XM jednakih ZK, i zamislimo na osi LM valjak OX kome su krugovi Op i FX osnove. Pa kroz tačke N i X konstruišemo ravni paralelne sa AB i GD i sa osnovama valjka OX i dobićemo krugove PS i TU sa centrima N i X. Pošto su ose LN, NE, EK jednake među sobom, odnosiće se valjci pP, PB, BH među sobom kao osnove [XII.11]. Ali i osnove su jednake. Prema tome su i valjci pP, PB, BH jednaki među sobom. Pošto su sad ose LN, NE, EK jednake među sobom, a i valjci pP, PB, BH među sobom, i broj jednih jednak je broju drugih, biće osa KL isti multiplum ose EK koji je i valjak pH multiplum valjka HB. Iz istih razloga je i osa MK isti multiplum ose KZ koji je i valjak XH valjka HD. I ako je osa KL jednaka osi KM, biće i valjak pH jednak valjku HX, ako je osa veća od ose, biće i valjak veći od valjka, i ako je manja, biće manji. Od četiri veličine, naime dve ose EK i KZ, i dva valjka BH i HD, naačinjeni su isti multiplumi, od ose EK i od valjka BH, osa LK i valjak pH, a od ose KZ i od valjka HD - osa KM i valjak HX, i dokazano je će, ako je osa KL veća od ose KM, biti i valjak pH veći od valjka HX, ako je jednaka, jednaki, a ako je manja, manji. Na ovaj način se osa EK odnosi prema osi KZ kao valjak BH prema valjku HD [V, Def. 5]. A to je trebalo dokazati.